GATE Theory of Computation PYQ
| Q1➡ | GATE 2021 Set-1 Suppose that L1is a regular language and L2is a context free language. Which one of the following languages is NOT necessarily context free? |
| i ➥ L1. L2 |
| ii ➥ L1 − L2 |
| iii ➥ L1 ∩ L2 |
| iv ➥ L1 ∪ L2 |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Closure Property | Help-Line |
| Q2➡ | GATE 2021 Set-1 Let denote an encoding of an automaton M. Suppose that Σ = {0,1}. Which of the following languages is/are NOT recursive? |
| i ➥ L = { | M is a PDA such that L(M) = ∅} |
| ii ➥ L = { | M is a PDA such that L(M) = Σ*} |
| iii ➥ L = { | M is a DFA such that L(M) = Σ*} |
| iv ➥ L = { | M is a DFA such that L(M) = ∅} |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Recursive Language | Help-Line |
| Q3➡ | GATE 2021 Set-1 For a Turing machine M, denotes an encoding of M. Consider the following two languages. L1=〈M〉|M takes more than 2021 steps on all inputs L2=〈M〉|M takes more than 2021 steps on some input Which one of the following options is correct? |
| i ➥ L1 is undecidable and L2 is decidable. |
| ii ➥ Both L1and L2 are decidable. |
| iii ➥ Both L1and L2 are undecidable. |
| iv ➥ L1 is decidable and L2 is undecidable. |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Decidability and Undecidability | Help-Line |
| Q4➡ | GATE 2021 Set-1 Consider the following language. L={w ∈{0,1}* | ends with the sub-string 011} Which one of the following deterministic finite automata accepts L ? |
| i ➥ |
ii ➥ 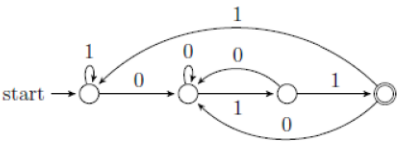 |
| iii ➥ |
| iv ➥ |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | DFA | Help-Line |
| Q5➡ | GATE 2021 Set-1 The number of strings of length 100 accepted by the above pushdown automaton is _____. |
Show Answer With Best Explanation
Answer: 50
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Push Down Automata | Help-Line |
| Q6➡ | GATE 2021 Set-2 Let L ⊆ {0, 1}* be an arbitrary regular language accepted by a minimal DFA with k states. Which one of the following languages must necessarily be accepted by a minimal DFA with k states? |
| i ➥ {0,1}* -L |
| ii ➥ L.L |
| iii ➥ L- {01} |
| iv ➥ L U {01} |
Show Answer With Best Explanation
Answer: I
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Deteministic Finite Automata | Help-Line |
| Q6➡ | GATE 2021 Set-2 Let L1 be a regular language and L2 be a context-free language. Which of the following languages is/are context free? |
| i ➥ |
| ii ➥ |
| iii ➥ |
| iv ➥ |
Show Answer With Best Explanation
Answer: I, II, IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Topic | Help-Line |
| Q7➡ | GATE 2021 Set-2 Consider the following deterministic finite automaton (DFA). The number of strings of length 8 accepted by the above automaton is ________. |
Show Answer With Best Explanation
Answer: 256
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | DFA | Help-Line |
| Q8➡ | GATE 2021 Set-2 Suppose we want to design a synchronous circuit that processes a string of 0’s and 1’s. Given a string, it produces another string by replacing the first 1 in any subsequence of consecutive 1’s by a 0. Consider the following example. Input sequence: 00100011000011100 Output sequence: 00000001000001100 A Mealy Machine is a state machine where both the next state and the output are functions of the present state and the current input. The above mentioned circuit can be designed as a two-state Mealy machine. The states in the Mealy machine can be represented using Boolean values 0 and 1. We denote the current state, the next state, the next incoming bit, and the output bit of the Mealy machine by the variables s, t, b and y respectively. Assume the initial state of the mealy machine is 0. What are the Boolean expressions corresponding to t and y in terms of s and b? |
| i ➥ |
| ii ➥ |
| iii ➥ |
| iv ➥ |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Mealy and Moore Machine | Help-Line |
| Q9➡ | GATE 2021 Set-2 Consider the following two statements about regular languages: S1: Every infinite regular language contains an undecidable language as a subset. S2: Every finite language is regular. Which one of the following choices is correct? |
| i ➥ Both S1 and S2 are true. |
| ii ➥ Neither S1 nor S2 is true. |
| iii ➥ Only S1 is true. |
| iv ➥ Only S2 is true. |
Show Answer With Best Explanation
Answer: I
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Regular Language | Help-Line |
| Q10➡ | GATE 2021 Set-2 Which of the following regular expressions represent(s) the set of all binary numbers that are divisible by three? Assume that the string ∊ is divisible by three. |
| i ➥ (0+11+11(1+00)*00)* |
| ii ➥ (0+1 (01*0)*1)* |
| iii ➥ (0+11+10(1+00)*01)* |
| iv ➥ (0*(1(01*0)*1)*)* |
Show Answer With Best Explanation
Answer: II, III, IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Regular Expression | Help-Line |
| Q11➡ | GATE 2021 Set-2 For a string w, we define wR to be the reverse of w. For example, if w = 01101 then wR= 10110. Which of the following languages is/are context-free? |
| i ➥ L={w x wR | w, x ∈ {0,1}* } |
| ii ➥ L={w x xR wR | w, x ∈ {0,1}* } |
| iii ➥ L={w x wR xR | w, x ∈ {0,1}* } |
| iv ➥ L={w wR x xR | w, x ∈ {0,1}* } |
Show Answer With Best Explanation
Answer: I, II, IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Context Free Language | Help-Line |
| Q12➡ | GATE 2020 Consider the language L = {an| n≥0} ∪ {anbn| n≥0} and the following statements. I. L is deterministic context-free. II. L is context-free but not deterministic context-free. III. L is not LL(k) for any k. Which of the above statements is/are TRUE? |
| i ➥ III only |
| ii ➥ I only |
| iii ➥ I and III only |
| iv ➥ II only |
Show Answer With Best Explanation
Answer: III
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Language and Grammers | Help-Line |
| Q13➡ | GATE 2020 Consider the following statements. I. If L1 ∪ L2 is regular, then both L1 and L2 must be regular. II. The class of regular languages is closed under infinite union. Which of the above statements is/are TRUE? |
| i ➥ II only |
| ii ➥ I only |
| iii ➥ Neither I nor II |
| iv ➥ Both I and II |
Show Answer With Best Explanation
Answer: III
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Regular Language | Help-Line |
| Q14➡ | GATE 2020 Which one of the following regular expressions represents the set of all binary strings with an odd number of 1’s? |
| i ➥ (0*10*10*)*0*1 |
| ii ➥ 10*(0*10*10*)* |
| iii ➥ (0*10*10*)*10* |
| iv ➥ ((0 + 1)*1(0 + 1)*1)*10* |
Show Answer With Best Explanation
Answer: Marks to All
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Regular Expression | Help-Line |
| Q15➡ | GATE 2020 Consider the following languages. L1 = {wxyx | w,x,y ∈ (0 + 1)+} L2 = {xy | x,y ∈ (a + b)*, |x| = |y|, x ≠ y} Which one of the following is TRUE? |
| i ➥ L1 is context-free but L2 is not context-free. |
| ii ➥ L1 is regular and L2 is context-free. |
| iii ➥ Neither L1 nor L2 is context-free. |
| iv ➥ L1 is context-free but not regular and L2 is context-free. |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Languages and Grammers | Help-Line |
| Q16➡ | GATE 2020 Which of the following languages are undecidable? Note that indicates encoding of the Turing machine M. L1 = {<M>| L(M) = Φ} L2 = {<M,w,q>| M on input w reaches state q in exactly 100 steps} L3 = {<M>| L(M) is not recursive} L4 = {<M>| L(M) contains at least 21 members} |
| i ➥ L2, L3 and L4 only |
| ii ➥ L1, L3 and L4 only |
| iii ➥ L2 and L3 only |
| iv ➥ L1 and L3 only |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Decidability & Undecidability | Help-Line |
| Q17➡ | GATE 2020 Consider the following language. L = {x ∈ {a,b}* | number of a’s in x is divisible by 2 but not divisible by 3} The minimum number of states in a DFA that accepts L is ______. |
Show Answer With Best Explanation
Answer: 6
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Finite Automata | Help-Line |
| Q18➡ | GATE 2019 If L is a regular language over Σ = {a,b}, which one of the following languages is NOT regular? |
| i ➥ L∙LR = {xy │ x ∈ L, yR ∈ L} |
| ii ➥ Suffix (L) = {y ∈ Σ*|∃y ∈ Σ* such that xy ∈ L} |
| iii ➥ Prefix (L) = {x ∈ Σ*│∃y ∈ Σ* such that xy ∈ L} |
| iv ➥ {wwR │w ∈ L} |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Regular Language | Help-Line |
| Q19➡ | GATE 2019 For Σ = {a,b}, let us consider the regular language L = {x|x = a2+3k or x = b10+12k, k ≥ 0}. Which one of the following can be a pumping length (the constant guaranteed by the pumping lemma) for L? |
| i ➥ 5 |
| ii ➥ 24 |
| iii ➥ 9 |
| iv ➥ 3 |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Regular Language | Help-Line |
| Q20➡ | GATE 2019 Consider the following sets: S1. Set of all recursively enumerable languages over the alphabet {0,1} S2. Set of all syntactically valid C programs S3. Set of all languages over the alphabet {0,1} S4. Set of all non-regular languages over the alphabet {0,1} Which of the above sets are uncountable? |
| i ➥ S1 and S2 |
| ii ➥ S3 and S4 |
| iii ➥ S2 and S3 |
| iv ➥ S1 and S4 |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Countability | Help-Line |
| Q21➡ | GATE 2019 Which one of the following languages over Σ = {a,b} is NOT context-free? |
| i ➥ {wanbnwR |w ∈ {a,b}*, n ≥ 0} |
| ii ➥ {anbi | i ∈ {n, 3n, 5n}, n ≥ 0} |
| iii ➥ {wanwRbn |w ∈ {a,b}*, n ≥ 0} |
| iv ➥ {wwR |w ∈ {a,b}*} |
Show Answer With Best Explanation
Answer: III
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Context Free Language | Help-Line |
| Q22➡ | GATE 2019 Let Σ be the set of all bijections from {1, …, 5} to {1, …, 5}, where id denotes the identity function i.e. id( j ) = j,∀j. Let º denote composition on functions. For a string x = x1 x2 … xn ∈ Σn, n ≥ 0. Let π(x) = x1 º x2 º … º xn. Consider the language L = {x ∈ Σ* | π(x) = id}. The minimum number of states in any DFA accepting L is _________. |
Show Answer With Best Explanation
Answer: 120
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Finite Automata | Help-Line |
| Q23➡ | GATE 2018 Let N be an NFA with n states. Let k be the number of states of a minimal DFA which is equivalent to N. Which one of the following is necessarily true? |
| i ➥ k ≤ n2 |
| ii ➥ k ≤ 2n |
| iii ➥ k ≥ 2n |
| iv ➥ k ≥ n |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | NFA/DFA | Help-Line |
| Q24➡ | GATE 2018 The set of all recursively enumerable languages is |
| i ➥ closed under complementation. |
| ii ➥ closed under intersection. |
| iii ➥ a subset of the set of all recursive languages. |
| iv ➥ an uncountable set. |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Closure-Property | Help-Line |
| Q25➡ | GATE 2018 |
| i ➥ I and IV only |
| ii ➥ I and II only |
| iii ➥ II and III only |
| iv ➥ II and IV only |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Context Free Language | Help-Line |
| Q26➡ | GATE 2018 Consider the following problems. L(G) denotes the language generated by a grammar G. L(M) denotes the language accepted by a machine M. (I) For an unrestricted grammar G and a string w, whether w∈L(G) (II) Given a Turing machine M, whether L(M) is regular (III) Given two grammar G1 and G2 whether L(G1 )=L(G2) (IV) Given an NFA N, whether there is a deterministic PDA P such that N and P accept the same language Which one of the following statement is correct? |
| i ➥ Only I and II are undecidable |
| ii ➥ Only III is undecidable |
| iii ➥ Only II and IV are undecidable |
| iv ➥ Only I, II and III are undecidable |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Undecidability | Help-Line |
| Q27➡ | GATE 2018 Given a language L, define Li as follows: L0 = {ε} Li = Li-1 ∙ L for all i>0 The order of a language L is defined as the smallest k such that Lk = Lk+1. Consider the language L1 (over alphabet 0) accepted by the following automaton. The order of L1 is __. |
Show Answer With Best Explanation
Answer: 2
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Finite Automata | Help-Line |
| Q28➡ | GATE 2017 Set-1 Consider the following context-free grammar over the alphabet Σ = {a, b, c} with S as the start symbol: S → abScT | abcT T → bT | b Which one of the following represents the language generated by the above grammar? |
| i ➥ {(ab)n (cbn)m│m,n ≥ 1} |
| ii ➥ {(ab)n (cb)n│n ≥ 1} |
| iii ➥ {(ab)n (cbm)n│m,n ≥ 1} |
| iv ➥ {(ab)n cbm1 cbm2 …cbmn │n,m1,m2,…,mn ≥ 1} |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Context Free Grammer | Help-Line |
| Q29➡ | GATE 2017 Set-1 Consider the language L given by the regular expression (a+b)*b(a+b) over the alphabet {a,b}. The smallest number of states needed in deterministic finite-state automation (DFA) accepting L is ________. |
Show Answer With Best Explanation
Answer: 4.0
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Finite Automata | Help-Line |
| Q30➡ | GATE 2017 Set-1 Consider the context-free grammars over the alphabet {a, b, c} given below. S and T are non-terminals. G1: S → aSb|T, T → cT|ϵ G2: S → bSa|T, T → cT|ϵ The language L(G1) ∩ L(G2) is |
| i ➥ Context-Free but not regular |
| ii ➥ Recursive but not context-free |
| iii ➥ Finite |
| iv ➥ Not finite but regular |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Context Free Grammer | Help-Line |
| Q31➡ | GATE 2017 Set-1 If G is a grammar with productions S → SaS | aSb | bSa | SS | ϵ where S is the start variable, then which one of the following strings is not generated by G? |
| i ➥ babba |
| ii ➥ abbaa |
| iii ➥ abab |
| iv ➥ aaab |
Show Answer With Best Explanation
Answer: I
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Grammer | Help-Line |
| Q32➡ | GATE 2017 Set-1 Let A and B be finite alphabets and let # be a symbol outside both A and B. Let f be a total function from A* to B*. We say f is computable if there exists a Turing machine M which given an input x in A, always halts with f(x) on its tape. Let Lf denote the language {x # f(x)│x ∈ A*}. Which of the following statements is true: |
| i ➥ If f is computable then Lf is recursively enumerable, but not conversely. |
| ii ➥ If f is computable then Lf is recursive, but not conversely. |
| iii ➥ f is computable if and only if Lf is recursive. |
| iv ➥ f is computable if and only if Lf is recursively enumerable. |
Show Answer With Best Explanation
Answer: III
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Computability | Help-Line |
| Q33➡ | GATE 2017 Set-1 Consider the following languages over the alphabet Σ = {a, b, c}. Let L1 = {an bn cm│m,n ≥ 0} and L2 = {am bn cn│m,n ≥ 0} Which of the following are context-free languages? I. L1∪ L2 II. L1∩ L2 |
| i ➥ II only |
| ii ➥ I only |
| iii ➥ Neither I nor II |
| iv ➥ I and II |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Context Free Language | Help-Line |
| Q34➡ | GATE 2017 Set-2 Let L1, L2 be any two context-free languages and R be any regular language. Then which of the following is/are CORRECT? I. L1 U L2 is context Free. II. III. L1 – R is context Free. IV. |
| i ➥ I only |
| ii ➥ I, II and IV only |
| iii ➥ II and IV only |
| iv ➥ I and III only |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Context Free language | Help-Line |
| Q35➡ | GATE 2017 Set-2 Identify the language generated by the following grammar, where S is the start variable. S → XY X → aX|a Y → aYb|ϵ |
| i ➥ {am bn │ m ≥ n, n > 0} |
| ii ➥ {am bn │ m ≥ n, n ≥ 0} |
| iii ➥ {am bn │ m > n, n ≥ 0} |
| iv ➥ {am bn │ m > n, n > 0} |
Show Answer With Best Explanation
Answer: III
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Finite Automata | Help-Line |
| Q36➡ | GATE 2017 Set-2 The minimum possible number of a deterministic finite automation that accepts the regular language L = {w1aw2 | w1, w2 ∈ {a,b}*, |w1| = 2,|w2| ≥ 3} is ___________. |
Show Answer With Best Explanation
Answer: 8
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | DFA | Help-Line |
| Q37➡ | GATE 2017 Set-2 Let L(R) be the language represented by regular expression R. Let L(G) be the language generated by a context free grammar G. Let L(M) be the language accepted by a Turing machine M. Which of the following decision problems are undecidable? • I. Given a regular expression R and a string w, is w ∈ L(R)? • II. Given a context-free grammar G, is L(G) = ∅? • III. Given a context-free grammar G, is L(G) = Σ* for some alphabet Σ? • IV. Given a Turing machine M and a string w, is w ∈ L(M)? |
| i ➥ III and IV only |
| ii ➥ II, III and IV only |
| iii ➥ II and III only |
| iv ➥ I and IV only |
Show Answer With Best Explanation
Answer: I
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Decidability and Undecidability | Help-Line |
| Q38➡ | GATE 2017 Set-2 Consider the following languages: L1 = {ap│p is a prime number} L2 = {an bmc2m | n ≥ 0, m ≥ 0} L3 = {an bn c2n │ n ≥ 0} L4 = {an bn │ n ≥ 1} Which of the following are CORRECT? I. L1 is context-free but not regular. II. L2 is not context-free. III. L3 is not context-free but recursive. IV. L4 is deterministic context-free. |
| i ➥ III and IV only |
| ii ➥ I and IV only |
| iii ➥ II and III only |
| iv ➥ I, II and IV only |
Show Answer With Best Explanation
Answer: I
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Context Free Language | Help-Line |
| Q39➡ | GATE 2017 Set-2 Let δ denote the transition function and Then |
| i ➥ {q0,q2,q3} |
| ii ➥ {q0,q1,q2} |
| iii ➥ {q0,q1,q3} |
| iv ➥ ∅ |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | NFA | Help-Line |
| Q40➡ | GATE 2016 Set-1 Which of the following languages is generated by the given grammar? S→ aS|bS|ε |
| i ➥ {a,b}* |
| ii ➥ {an |n ≥ 0} U {bn |n ≥ 0} U {an bn|n ≥ 0} |
| iii ➥ {w ∈ {a,b}* | w has equal number of a’s and b’s} |
| iv ➥ {anbm |n,m ≥ 0} |
Show Answer With Best Explanation
Answer: I
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Language | Help-Line |
| Q41➡ | GATE 2016 Set-1 Which of the following decision problems are undecidable? • I. Given NFAs N1 and N2, is L(N1)∩L(N2)= Φ? • II. Given a CFG G = (N,Σ,P,S) and a string x ∈ Σ*, does x ∈ L(G)? • III. Given CFGs G1 and G2, is L(G1) = L(G2)? • IV. Given a TM M, is L(M) = Φ? |
| i ➥ II and IV only |
| ii ➥ III and IV only |
| iii ➥ II and III only |
| iv ➥ I and IV only |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Decidability and Undecidability | Help-Line |
| Q42➡ | GATE 2016 Set-1 Which one of the following regular expressions represents the language: the set of all binary strings having two consecutive 0s and two consecutive 1s? |
| i ➥ 00(0 + 1)* 11 + 11(0 + 1)* 00 |
| ii ➥ (0 + 1)* 00(0 + 1)* + (0 + 1)* 11(0 + 1)* |
| iii ➥ (0 + 1)* (00(0 + 1)* 11 + 11(0 + 1)* 00)(0 + 1)* |
| iv ➥ (0 + 1)* 0011(0 + 1)* + (0 + 1)* 1100(0 + 1)* |
Show Answer With Best Explanation
Answer: III
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Regular Expressions | Help-Line |
| Q42➡ | GATE 2016 Set-1 Consider the following context-free grammars: G1: S → aS|B, B → b|bB G2: S → aA|bB, A → aA|B|ε, B → bB|ε Which one of the following pairs of languages is generated by G1 and G2, respectively? |
| i ➥ {am bn│m > 0 or n > 0} and {am bn |m > 0 and n > 0} |
| ii ➥ {am bn│m > 0 and n > 0} and {am bn |m > 0 or n≥0} |
| iii ➥ {am bn│m≥0 or n > 0} and {am bn |m > 0 and n > 0} |
| iv ➥ {am bn│m≥0 and n > 0} and {am bn |m > 0 or n > 0} |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Context Free Language | Help-Line |
| Q43➡ | GATE 2016 Set-1 Consider the transition diagram of a PDA given below with input alphabet Σ = {a,b} and stack alphabet Γ = {X,Z}. Z is the initial stack symbol. Let L denote the language accepted by the PDA. Which one of the following is TRUE? |
| i ➥ L = {an bn│n ≥ 0} and is not accepted by any finite automata |
| ii ➥ L = {an |n≥0} ∪ {anbn|n ≥ 0} and is not accepted by any deterministic PDA |
| iii ➥ L is not accepted by any Turing machine that halts on every input |
| iv ➥ L = {an |n ≥ 0} ∪ {an bn |n ≥ 0} and is deterministic context-free |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Push Down Automata | Help-Line |
| Q44➡ | GATE 2016 Set-2 The number of states in the minimum sized DFA that accepts the language defined by the regular expression (0+1)*(0+1) (0+1)* is_________. |
Show Answer With Best Explanation
Answer: 2
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | DFA | Help-Line |
| Q45➡ | GATE 2016 Set-2 Language L1 is defined by the grammar: S1 → aS1b|ε Language L2 is defined by the grammar: S2 → abS2|ε Consider the following statements: • P: L1 is regular • Q: L2 is regular Which one of the following is TRUE? |
| i ➥ Both P and Q are true |
| ii ➥ P is true and Q is false |
| iii ➥ P is false and Q is true |
| iv ➥ Both P and Q are false |
Show Answer With Best Explanation
Answer: III
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Regular Language | Help-Line |
| Q46➡ | GATE 2016 Set-2 Consider the following types of languages: L1: Regular, L2: Context-free, L3 : Recursive, L4 : Recursively enumerable. Which of the following is/are TRUE? |
| i ➥ I only |
| ii ➥ I and III only |
| iii ➥ I and IV only |
| iv ➥ I, II and III only |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Closure Property | Help-Line |
| Q47➡ | GATE 2016 Set-2 Consider the following two statements: I: If all states of an NFA are accepting states then the language accepted by the NFA is Σ*. II: There exists a regular language A such that for all languages B, A∩B is regular. Which one of the following is CORRECT? |
| i ➥ Only I is true |
| ii ➥ Only II is true |
| iii ➥ Both I and II are true |
| iv ➥ Both I and II are false |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Finite Automata and Regular Language | Help-Line |
| Q48➡ | GATE 2016 Set-2 Consider the following languages: • L1= {an bm cn+m : m,n ≥ 1} • L2= {an bn c2n : n ≥ 1} Which one of the following is TRUE? |
| i ➥ Both L1 and L2 are context-free. |
| ii ➥ L1 is context-free while L2 is not context-free. |
| iii ➥ L2 is context-free while L1 is not context-free. |
| iv ➥ Neither L1 nor L2 is context-free. |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Context Free Language | Help-Line |
| Q49➡ | GATE 2016 Set-2 Consider the following languages. • L1 = {〈M〉|M takes at least 2016 steps on some input}, • L2 = {〈M〉│M takes at least 2016 steps on all inputs} and • L3 = {〈M〉|M accepts ε}, where for each Turing machine M, 〈M〉 denotes a specific encoding of M. Which one of the following is TRUE? |
| i ➥ L1 is recursive and L2, L3 are not recursive |
| ii ➥ L2 is recursive and L1, L3 are not recursive |
| iii ➥ L1, L2 are recursive and L3 is not recursive |
| iv ➥ L1, L2, L3 are recursive |
Show Answer With Best Explanation
Answer: III
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Recursive Language | Help-Line |
| Q50➡ | GATE 2015 Set-1 For any two languages L1 and L2 such that L1 is context-free and L2 is recursively enumerable but not recursive, which of the following is/are necessarily true? I. L’1 (Complement of L1) is recursive. II. L’2 (Complement of L2) is recursive. III. L’1 is context Free IV. L’1 U L2 is recursive Enumerable. |
| i ➥ I only |
| ii ➥ III only |
| iii ➥ III and IV only |
| iv ➥ I and IV only |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Languages | Help-Line |
| Q51➡ | GATE 2015 Set-1 Consider the DFAs M and N given above. The number of states in a minimal DFA that accepts the language L(M) ∩ L(N) is _____. |
Show Answer With Best Explanation
Answer: 1
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | DFA | Help-Line |
| Q52➡ | GATE 2015 Set-1 Consider the NPDA 〈Q = {q0, q1, q2}, Σ = {0, 1}, Γ = {0, 1, ⊥}, δ, q0, ⊥, F = {q2}〉, where (as per usual convention) Q is the set of states, Σ is the input alphabet, Γ is stack alphabet, δ is the state transition function, q0 is the initial state, ⊥ is the initial stack symbol, and F is the set of accepting states, The state transition is as follows: Which one of the following sequences must follow the string 101100 so that the overall string is accepted by the automaton? |
| i ➥ 10110 |
| ii ➥ 10010 |
| iii ➥ 01010 |
| iv ➥ 01001 |
Show Answer With Best Explanation
Answer: II
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | PDA | Help-Line |
| Q53➡ | GATE 2015 Set-2 Consider the following statements: I. The complement of every Turning decidable language is Turning decidable II. There exists some language which is in NP but is not Turing decidable III. If L is a language in NP, L is Turing decidable Which of the above statements is/are True? |
| i ➥ Only II |
| ii ➥ Only III |
| iii ➥ Only I and II |
| iv ➥ Only I and III |
Show Answer With Best Explanation
Answer: IV
Explanation: Upload Soon
| More Discussion | Explanation On YouTube | Decidability and Undecidability | Help-Line |
| Q54➡ | |