Two Dimensional Array in Data Structure
Two Dimension Array Address Calculation
# Two dimensional arrays are called matrices in mathematical and tables in business application.
# Two D- arrays are also called matrix arrays. # We are having standard way of drawing a two-dimensional m X n array P. where m is row and n is column.
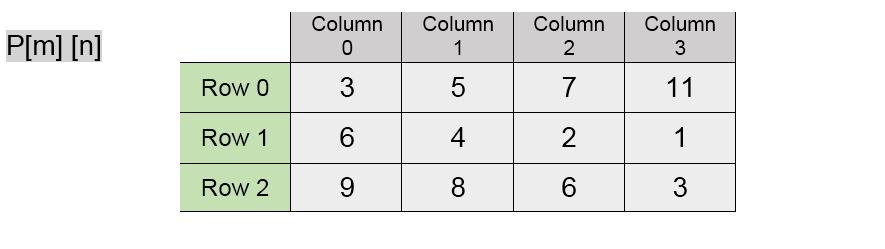
| • The number of rows or columns is called the range of the dimension. In the array a. the Range of the first dimension is 3 and the range of the second dimension is 4.Thus array has three rows and four columns. |
| • To implement a two-dimensional array, it is necessary to develop a method of ordering its ele-ments in a linear fashion and of transforming a two-dimensional reference to the linear representation. There are two methods of representing a two dimension array in memory. 1st row-major representation 2nd column- major representation |
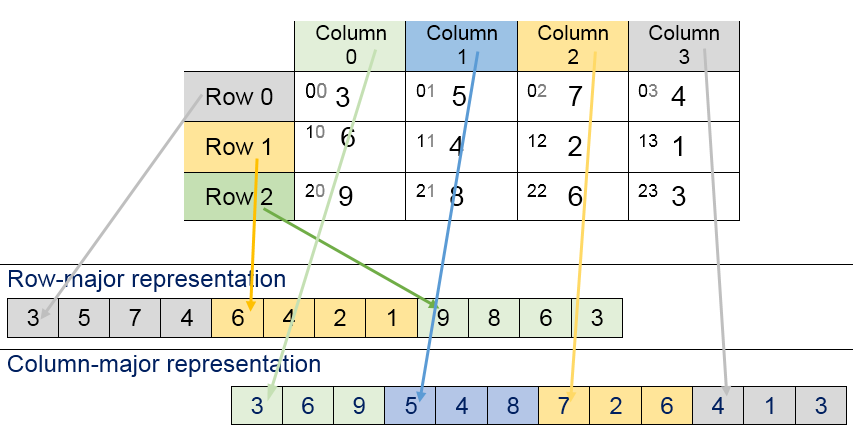
| Address of an element “P[ I ][ J ]” is calculated in two forms 1st Row Major 2nd Column Major Formula for calculate address in Row Major Order M:N Address of P [ I ][ J ] = [((( I – LBr )*N) + ( J – LBc ))* W + Base] Formula for calculate address in Column Major Order M:N Address of P [ I ][ J ] = [((( J – LBc )*M)+ ( I – LBr ))* W + Base] Find the numbers of row and Column. Number of rows (M) will be calculated as = (UBr – LBr) + 1 Number of columns (N) will be calculated as =(UBc – LBc) + 1 | Where, B = Base address. I = Row subscript of element whose address is to be found. J = Column subscript of element whose address is to be found. W = Storage Size of one element stored in the array (in byte). LBr = Lower limit of row/start row index of matrix, if not given assume 0 (zero). LBc = Lower bound of column/start column in of matrix, if not given assume 0 (zero). M = Number of row of the given matrix. N = Number of column of the given matrix. |
