NTA UGC NET Linear Programming Problems Question with Solutions
| Q.1➡ | UGC NET DEC 2023 Comprehension: Food X contains 6 units of Vitamin D per gram and 7 units of Vitamin E per gram and cost is Rs 12 per gram. Food Y contains 8 units of vitamin D per gram and 12 units of Vitamin E per gram and cost is Rs 20 per gram. The daily minimum requirements of vitamin D and E are 100 units and 120 units respectively. Suppose x is quantity (in gram) of food X, y is quantity (in gram) of food Y. Answering the following question based on the above paragraph given. The cost function of total food is : |
| i ➥ Z = 6x + 7y |
| ii ➥ Z = 8x + 12y |
| iii ➥ Z = 12x + 20y |
| iv ➥ Z = 20x + 12y |
| Best Explanation: Answer: (III) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.2➡ | UGC NET DEC 2023 Comprehension: Food X contains 6 units of Vitamin D per gram and 7 units of Vitamin E per gram and cost is Rs 12 per gram. Food Y contains 8 units of vitamin D per gram and 12 units of Vitamin E per gram and cost is Rs 20 per gram. The daily minimum requirements of vitamin D and E are 100 units and 120 units respectively. Suppose x is quantity (in gram) of food X, y is quantity (in gram) of food Y. Answering the following question based on the above paragraph given. The dual of the formulated LPP is: |
i ➥ 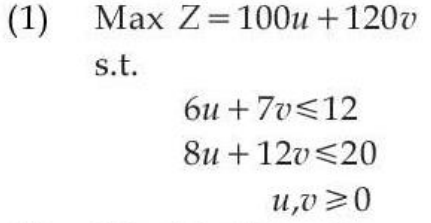 = 0″> = 0″> |
ii ➥ 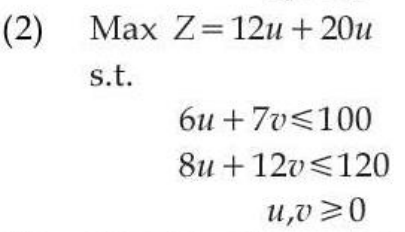 = 0″> = 0″> |
iii ➥ 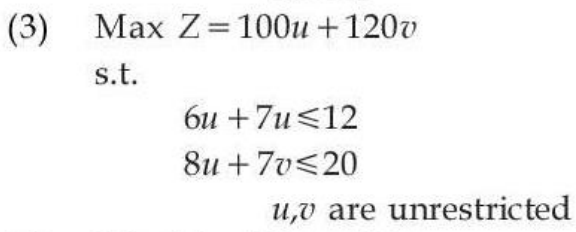 |
iv ➥ 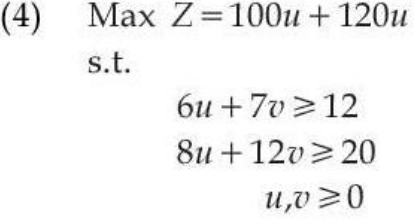 = 12
8u + 12v >= 20
u, v >= 0″> = 12
8u + 12v >= 20
u, v >= 0″> |
| Best Explanation: Answer: (I) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.3➡ | UGC NET DEC 2023 Comprehension: Food X contains 6 units of Vitamin D per gram and 7 units of Vitamin E per gram and cost is Rs 12 per gram. Food Y contains 8 units of vitamin D per gram and 12 units of Vitamin E per gram and cost is Rs 20 per gram. The daily minimum requirements of vitamin D and E are 100 units and 120 units respectively. Suppose x is quantity (in gram) of food X, y is quantity (in gram) of food Y. Answering the following question based on the above paragraph given. Which of the following constrains when formulating the LPP ? |
| i ➥ 6x + 7y <= 100, 8x + 12y <= 120, x, y >= 0 |
| ii ➥ 6x + 8y <= 100, 7x + 12y <= 120, x, y >= 0 |
| iii ➥ 6x + 7y >= 100, 8x + 12y >= 120, x, y >= 0 |
| iv ➥ 6x + 8y >= 100, 7x + 12y >= 120, x, y >= 0 |
| Best Explanation: Answer: (IV) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.4➡ | UGC NET DEC 2023 Comprehension: Food X contains 6 units of Vitamin D per gram and 7 units of Vitamin E per gram and cost is Rs 12 per gram. Food Y contains 8 units of vitamin D per gram and 12 units of Vitamin E per gram and cost is Rs 20 per gram. The daily minimum requirements of vitamin D and E are 100 units and 120 units respectively. Suppose x is quantity (in gram) of food X, y is quantity (in gram) of food Y. Answering the following question based on the above paragraph given. Which of the following are quantities (in grams) of food X and Y respectively when the cost of food is minimum: |
| i ➥ |
| ii ➥ |
| iii ➥ |
| iv ➥ 0 and 10 |
| Best Explanation: Answer: (II) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.5➡ | UGC NET DEC 2023 Comprehension: Food X contains 6 units of Vitamin D per gram and 7 units of Vitamin E per gram and cost is Rs 12 per gram. Food Y contains 8 units of vitamin D per gram and 12 units of Vitamin E per gram and cost is Rs 20 per gram. The daily minimum requirements of vitamin D and E are 100 units and 120 units respectively. Suppose x is quantity (in gram) of food X, y is quantity (in gram) of food Y. Answering the following question based on the above paragraph given. The minimum cost of food is : |
| i ➥ 205 |
| ii ➥ 250 |
| iii ➥ 330 |
| iv ➥ 200 |
| Best Explanation: Answer: (I) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.6➡ | UGC NET JUNE 2023 Match List I with List II 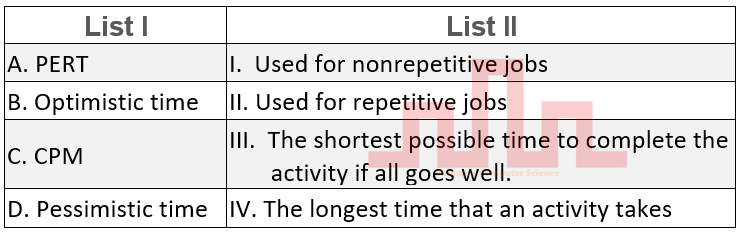 Choose the correct answer from the options given below: |
| i ➥ A-III B-IV C-II D-I |
| ii ➥ A-IV B-I C-I D-III |
| iii ➥ A-I B-III C-II D-III |
| iv ➥ A-I B-III C-II D-IV |
| Best Explanation: Answer: IV Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.7➡ | UGC NET JUNE 2023 How many integral solutions are there to x + y + z + w = 29 ,where x >= 1, y >= 2, z >= 3 and w >= 0 ? |
| i ➥ 2400 |
| ii ➥ 2600 |
| iii ➥ 2800 |
| iv ➥ 3000 |
| Best Explanation: Answer: II Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.8➡ | UGC NET JUNE 2023 How will you free the memory allocated by the following program? include stdio.h include stdlib.h define MAXROW 3 define MAXCOL 4 int main() { int **p, i, j; p = (int **) malloc(MAXROW * sizeof(int*)); return 0; } |
| i ➥ memfree (int p); |
| ii ➥ dealloc (p); |
| iii ➥ malloc (p,0); |
| iv ➥ free (p); |
| Best Explanation: Answer: IV Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.9➡ | UGC NET JUNE 2023 There are M points on one straight line AB and n points on another straight line AC none of them being A. How many triangles can be formed with these points as vertices? |
| i ➥ mn(m + n – 2) |
| ii ➥ 1/2 * mn(m + n – 2) |
| iii ➥1/2 * mn(m + n – 1) |
| iv ➥mn(m + n – 1) |
| Best Explanation: Answer: II Explanation: The task is to find the number of triangles that can be formed using the given points on two straight lines AB and AC, where there are M points on line AB and n points on line AC (none of them being A). To form a triangle, we need to choose three points—one from each line. Let’s go through the reasoning for the correct answer: Option ii. 1/2 * mn(m + n – 2) : 1/2: This factor accounts for the fact that choosing points A, B, and C is the same as choosing points A, C, and B. It eliminates overcounting. mn: This part represents the number of ways to choose one point from line AB (M choices) and one point from line AC (n choices). (m+n−2): This part represents the number of ways to choose the third point, considering that the chosen points cannot be A. There are M + n points in total, and we subtract 2 (A and one of the chosen points) to ensure that the third point is not A and is distinct from the chosen points on AB and AC. Putting it all together, 1/2*mn(m+n−2) gives the correct count of non-degenerate triangles formed by choosing three points from the given lines. This expression accounts for the necessary combinations and avoids overcounting, making it a suitable formula for calculating the number of triangles. Therefore, option ii is the correct answer: 1/2*mn(m+n−2) |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.10➡ | NTA UGC NET November 2020  |
| i ➥ 23 |
| ii ➥ 9.5 |
| iii ➥ 13 |
| iv ➥ 8 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.11➡ | NTA UGC NET December 2019  |
| i ➥ x1=750, x2=750, z=1500 |
| ii ➥ x1=500, x2=100, z=1500 |
| iii ➥ x1=1000, x2=500, z=1500 |
| iv ➥ x1=900, x2=600, z=1500 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.12➡ | NTA UGC NET December 2019 Consider the following statements with respect to duality in LPP: (a) The final simplex table giving optimal solution of the primal also contains optimal solution of its dual in itself. (b) If either the primal or the dual problem has a finite optimal solution, then the other problem also has a finite optimal solution. (c) If either problem has an unbounded optimal solution, then the other problem has no feasible solution at all. Which of the statements is (are) correct? |
| i ➥ only (a) and (b) |
| ii ➥ only (a) and (c) |
| iii ➥ only (b) and (c) |
| iv ➥ (a), (b) and (c) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.13➡ | NTA UGC NET December 2019 A basic feasible solution of an mXn Transportation-Problem is said to be non-degenerate, if basic feasible solution contains exactly____number of individual allocation in ___positions |
| i ➥ m+n+1, independent |
| ii ➥ m+n-1, independent |
| iii ➥ m+n-1, appropriate |
| iv ➥ m-n+1, independent |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.14➡ | NTA UGC NET JUNE 2019  |
| i ➥ x1=5/2, x2=0, x3=0, Z=5 |
| ii ➥ x1=0, x2=0, x3=5/2, Z=5 |
| iii ➥ x1=0, x2=5/2, x3=0, Z= -5/2 |
| iv ➥ x1=0, x2=0, x3=10, Z=20 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.15➡ | NTA UGC NET December 2018 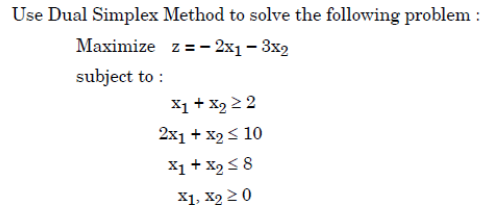 |
| i ➥ x1 =2, x2 =0 and z = -4 |
| ii ➥ x1 =2, x2 =6 and z = -22 |
| iii ➥ x1 =0, x2 =2 and z = -6 |
| iv ➥ x1 =6, x2 =2 and z = -18 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.16➡ | NTA UGC NET JUNE 2018 Which of the following statements is false about convex minimization problem ? |
| i ➥ If a local minimum exists, then it is a global minimum |
| ii ➥ The set of all global minima is convex set |
| iii ➥ The set of all global minima is concave set |
| iv ➥ For each strictly convex function, if the function has a minimum, then the minimum is unique |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.17➡ | NTA UGC NET JUNE 2018 The following LPP Maximize z=100x1+2x2 +5x3 Subject to 14x1+x2 −6x3 +3x4 =7 32x1 +x2 −12x3 ≤10 3x1 −x2 −x3 ≤0 x1 , x2 , x3 , x4 ≥ 0 has |
| i ➥ x1 =100, x2 =0, x3 =0 |
| ii ➥ Unbounded solution |
| iii ➥ No solution |
| iv ➥ x1 =50, x2 =70, x3 =60 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.18➡ | NTA UGC NET November 2017 Paper -3 Which of the following is a valid reason for causing degeneracy in a transportation problem ? Here m is no. of rows and n is no. of columns in transportation table |
| i ➥ When the number of allocations is m+n−1. |
| ii ➥ When two or more occupied cells become unoccupied simultaneously. |
| iii ➥ When the number of allocations is less than m+n−1. |
| iv ➥ When a loop cannot be drawn without using unoccupied cells, except the starting cell of the loop. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.19➡ | NTA UGC NET November 2017 Paper -3 Consider the following LPP : Max Z = 15x1 + 10x2 Subject to the constraints 4x1 + 6x2 ≤ 360 3x1 + 0x2 ≤ 180 0x1 + 5x2 ≤ 200 x1, x2 / 0 The solution of the LPP using Graphical solution technique is : |
| i ➥ x1=60, x2=0 and Z=900 |
| ii ➥ x1=60, x2=20 and Z=1100 |
| iii ➥ x1=60, x2=30 and Z=1200 |
| iv ➥ x1=50, x2=40 and Z=1150 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.20➡ | NTA UGC NET November 2017 Paper -3 Consider the following LPP : Min Z = 2x1 + x2 + 3x3 Subject to : x1 − 2x2 + x3 ≥ 4 2x1 + x2 + x3 ≤ 8 x1 − x3 ≥ 0 x1, x2, x3 ≥ 0 The solution of this LPP using Dual Simplex Method is : |
| i ➥ x1=0, x2=0, x3=3 and Z=9 |
| ii ➥ x1=0, x2=6, x3=0 and Z=6 |
| iii ➥ x1=4, x2=0, x3=0 and Z=8 |
| iv ➥ x1=2, x2=0, x3=2 and Z=10 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.21➡ | NTA UGC NET January 2017 Paper -3 Which of the following statements is true? |
| i ➥ The sentence S is a logical consequence of S1,…., Sn if and only if S1 ∧ S2 ∧…. ∧ Sn → S is satisfiable. |
| ii ➥ The sentence S is a logical consequence of S1,…., Sn if and only if S1 ∧ S2 ∧…. ∧ Sn → S is valid. |
| iii ➥ The sentence S is a logical consequence of S1,…., Sn if and only if S1 ∧ S2 ∧…. ∧ Sn → S is consistent. |
| iv ➥ The sentence S is a logical consequence of S1,…., Sn if and only if S1 ∧ S2 ∧…. ∧ Sn → S is inconsistent. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.22➡ | NTA UGC NET January 2017 Paper -3 A t-error correcting q-nary linear code must satisfy: 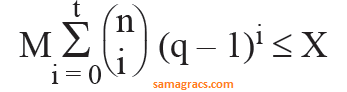 Where M is the number of code words and X is |
| i ➥ qn |
| ii ➥ qt |
| iii ➥ q-n |
| iv ➥ q-t |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.23➡ | NTA UGC NET January 2017 Paper -3 With respect to a loop in the transportation table, which one of the following is not correct? |
| i ➥ Every loop has an odd no. of cells and at least 5. |
| ii ➥ Closed loops may or may not be square in shape. |
| iii ➥ All the cells in the loop that have a plus or minus sign, except the starting cell, must be occupied cells. |
| iv ➥ Every loop has an even no. of cells and at least four |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.24➡ | NTA UGC NET January 2017 Paper -3 At which of the following stage(s), the degeneracy do not occur in transportation problem ? (m, n represents number of sources and destinations respectively) (1) While the values of dual variables ui and vj cannot be computed. (2) While obtaining an initial solution, we may have less than m + n – 1 allocations. (3) At any stage while moving towards optimal solution, when two or more occupied cells with the same minimum allocation become unoccupied simultaneously. (4) At a stage when the no. of +ve allocation is exactly m + n – 1. |
| i ➥ (a), (b) and (c) |
| ii ➥ (a), (c) and (d) |
| iii ➥ (a) and (d) |
| iv ➥ (a), (b), (c) and (d) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.25➡ | NTA UGC NET January 2017 Paper -3 Consider the following LPP : 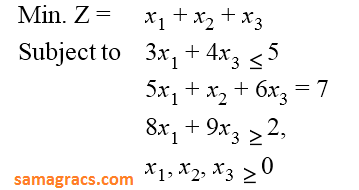 The standard form of this LPP shall be : |
i ➥ 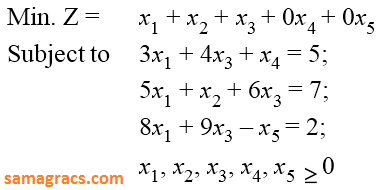 |
ii ➥ 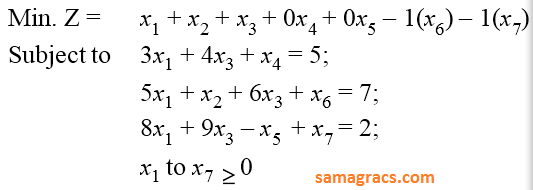 |
iii ➥ 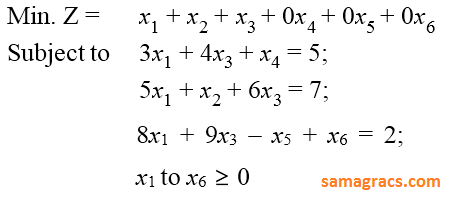 |
iv ➥ 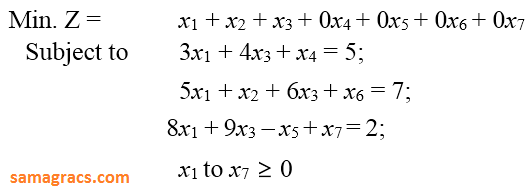 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.26➡ | NTA UGC NET August 2016 Paper -3 Which of the following is used for the boundary representation of an image object? |
| i ➥ Quad Tree |
| ii ➥ Projections |
| iii ➥ Run length coding |
| iv ➥ Chain codes |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.27➡ | NTA UGC NET August 2016 Paper -3 The region of feasible solution of a linear programming problem has a _ property in geometry, provided the feasible solution of the problem exists. |
| i ➥ concavity |
| ii ➥ convexity |
| iii ➥ quadratic |
| iv ➥ polyhedron |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.28➡ | NTA UGC NET August 2016 Paper -3 Consider the following statements: (1) Revised simplex method requires lesser computations than the simplex method. (2) Revised simplex method automatically generates the inverse of the current basis matrix. (3) Less number of entries are needed in each table of revised simplex method than usual simplex method. Which of these statements are correct? |
| i ➥ (1) and (2) only |
| ii ➥ (1) and (3) only |
| iii ➥ (2) and (3) only |
| iv ➥ (1), (2) and (3) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.29➡ | NTA UGC NET August 2016 Paper -3 The following transportation problem: is 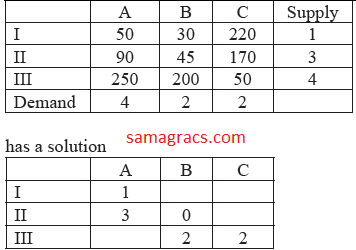 The above solution of a given transportation problem is: |
| i ➥ infeasible solution |
| ii ➥ optimum solution |
| iii ➥ non-optimum solution |
| iv ➥ unbounded solution |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.30➡ | NTA UGC NET December 2015 Paper -3 A basic feasible solution of a linear programming problem is said to be __ if at least one of the basic variables is zero. |
| i ➥ Degenerate |
| ii ➥ non-degenerate |
| iii ➥ Infeasible |
| iv ➥ Unbounded |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.31➡ | NTA UGC NET December 2015 Paper -3 Consider the following conditions: (a)The solution must be feasible, i.e. it must satisfy all the supply and demand constraints. (b)The number of positive allocations must be equal to m+n-1, where m is the number of rows and n is the number of columns. (c)All the positive allocations must be in independent positions. The initial solution of a transportation problem is said to be non-degenerate basic feasible solution if it satisfies: |
| i ➥ (a) and (b) only |
| ii ➥ (a) and (c) only |
| iii ➥ (b) and (c) only |
| iv ➥ (a), (b) and (c) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.32➡ | NTA UGC NET December 2015 Paper -3 Consider the following transportation problem: 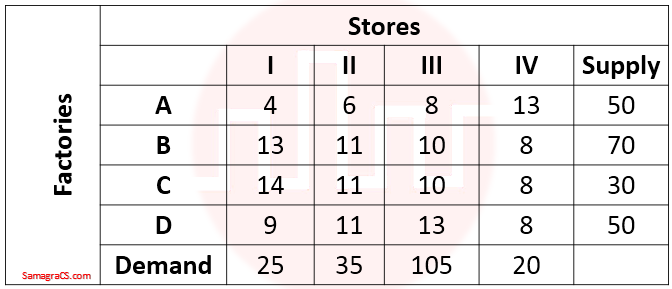 The transportation cost in the initial basic feasible solution of the above transportation problem using Vogel’s Approximation method is: |
| i ➥ 1450 |
| ii ➥ 1465 |
| iii ➥ 1480 |
| iv ➥ 1520 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.33➡ | NTA UGC NET June 2015 Paper -3 In the Hungarian method for solving assignment problem, an optimal assignment requires that the maximum number of lines that can be drawn through squares with zero opportunity cost is equal to the number of: |
| i ➥ rows or columns |
| ii ➥ rows + columns |
| iii ➥ rows + columns – 1 |
| iv ➥ rows + columns + 1 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.34➡ | NTA UGC NET June 2015 Paper -3 Given the following statements with respect to linear programming problem: S1 : The dual of the dual linear programming problem is again the primal problem S2 : If either the primal or the dual problem has an unbounded objective function value, the other problem has no feasible solution. S3 : If either the primal or dual problem has a finite optimal solution, the other one also possesses the same, and the optimal value of the objective functions of the two problems are equal. Which of the following is true? |
| i ➥ S1 and S2 |
| ii ➥ S1 and S3 |
| iii ➥ S2 and S3 |
| iv ➥ S1 , S2 and S3 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.35➡ | NTA UGC NET June 2015 Paper -3 Consider the following transportation problem: 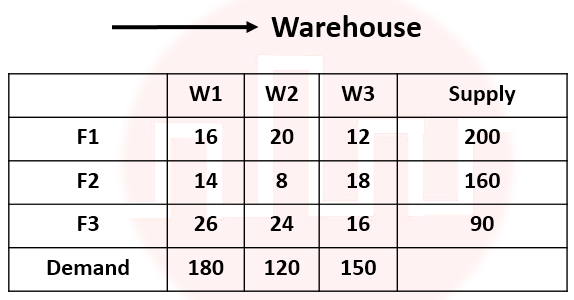 The initial basic feasible solution of the above transportation problem using Vogel’s Approximation Method (VAM) is given below: 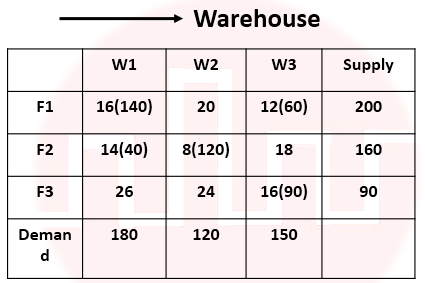 The solution of the above problem. |
| i ➥ is degenerate solution |
| ii ➥ is optimum solution |
| iii ➥ needs to improve |
| iv ➥ is infeasible solution |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
DO more practice
NTA UGC NET Subject Wise Previous Year Question With Solutions
