Theory of Computation Subject Wise UGC NET Question Analysis
| Q.1➡ | UGC NET DEC 2023 Let L={ab, aa, baa}. Which of the following strings are not in L*. |
| i ➥ abaabaaabaa |
| ii ➥ aaaabaaaa |
| iii ➥ baaaaabaaaab |
| iv ➥ baaaaabaa |
| Best Explanation: Answer: (III) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.2➡ | UGC NET DEC 2023 Choose the correct answer from the options given below |
| i ➥ (A)-(1), (B)-(II), (C)-(III), (D)-(IV) |
| ii ➥ (A)-(II), (B)-(I), (C)-(III), (D)-(IV) |
| iii ➥ (A)-(II), (B)-(I), (C)-(IV), (D)-(III) |
| iv ➥ (A)-(I), (B)-(II), (C)-(IV), (D)-(III) |
| Best Explanation: Answer: (IV) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.3➡ | UGC NET DEC 2023 Which of the statement is/are CORRECT ? (A) Moore and Mealy machines are finite state machines with output capabilities. (B) Any given Moore machine has an equivalent Mealy machine. (C) Any given Mealy machine has an equivalent Moore machine. (D) Moore machine is not a finite state machine. Choose the correct answer from the options given below : |
| i ➥ (A) and (B) Only |
| ii ➥ (A), (B) and (C) Only |
| iii ➥ (B) and (D) Only |
| iv ➥ (A), (B) and (D) Only |
| Best Explanation: Answer: (II) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.4➡ | UGC NET DEC 2023 Which of the following is not a palindromic subsequence of the string “ababcdabba” ? |
| i ➥ abcba |
| ii ➥ abba |
| iii ➥ abbbba |
| iv ➥ adba |
| Best Explanation: Answer: (IV) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.5➡ | UGC NET DEC 2023 The sum of minimum and maximum number of final states for a Deterministic Finite Automata (DFA) having ‘P’ state is equal to: |
| i ➥ P |
| ii ➥ p-1 |
| iii ➥ p + 1 |
| iv ➥ p + 2 |
| Best Explanation: Answer: (III) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.6➡ | UGC NET DEC 2023 Let A={a, b} and L=A*. Let x={anbn, n>0}. The languages L ⋃ X and X are respectively : |
| i ➥ Not regular, Regular |
| ii ➥ Regular, Regular |
| iii ➥ Regular, Not regular |
| iv ➥ Not Regular, Not Regular |
| Best Explanation: Answer: (III) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
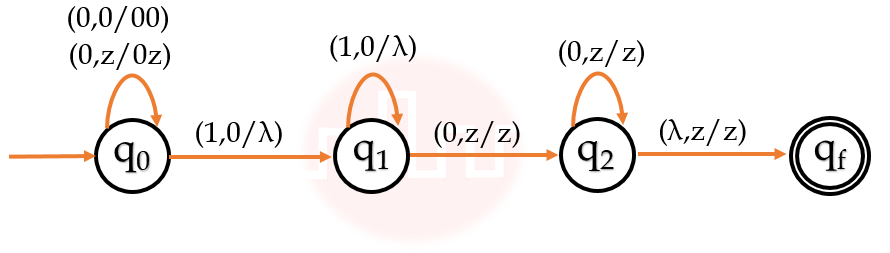
| Q.7➡ |UGC NET JUNE 2023 Consider the following finite automata F1 that accepts a language L 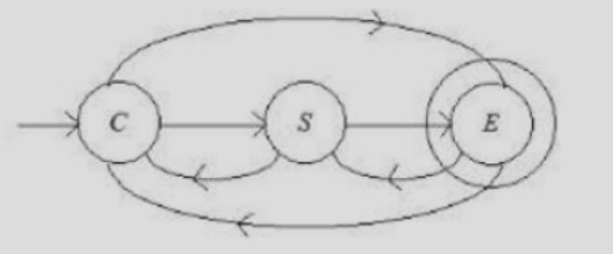 Let F2 be a finite automata which is obtained by reversal of F1. Then which of the following is correct? |
| i ➥ L(F1) ≠ L(F2) |
| ii ➥ L (F1)=L(F2) |
| iii ➥ L (F1)≤ L(F2) |
| iv ➥ L (F1)≥ L(F2) |
| Best Explanation: Answer: II Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.8➡ | UGC NET JUNE 2023 Consider following statements: A. A context free language is generated by LR(0) grammar if and only if it is accepted by a deterministic pushdown automata and has prefix property B. If M1 is the single tape TM simulating multilape TM M, then time taken by M1 to simulate n moves is (n3 ) C. Push down automata behaves like a Turning machine when it has one auxiliary memory. D. L={anbncn:n≥1} is not context free but context sensitive. Choose the correct answer from the options given below: |
| i ➥ A, B and C only |
| ii ➥ A, B only |
| iii ➥ C, D only |
| iv ➥ B, C only |
| Best Explanation: Answer: IV Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.9➡ | UGC NET JUNE 2023 A. The set of turning machine codes for TM’s that accept all inputs that are palindromes (possible along with some other inputs) is decidable B. The language of codes for TM’s M that when started with blank tape, eventually write a 1 somewhere on the tape is undecidable C. The language accepted by a TM M is L (M) is always recursive D. Post’s correspondence problem is undecidable Choose the correct answer from the options given below: |
| i ➥ A, B and C only |
| ii ➥ B, C and D only |
| iii ➥ A and C only |
| iv ➥ B and D only |
| Best Explanation: Answer: IV Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.10➡ | UGC NET JUNE 2023 Consider the following language: 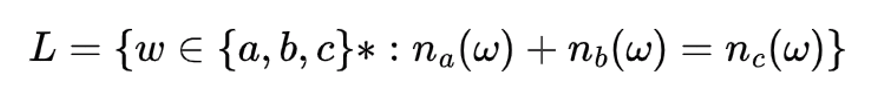 L is… |
| i ➥ Context free but not linear |
| ii ➥ Not context free |
| iii ➥ Context free and linear |
| iv ➥ Linear |
| Best Explanation: Answer: I Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.11➡ | UGC NET JUNE 2023 Given below are two statements: Statement I: If f and g are two functions and f = O(g) but g≠o(f), we say that the growth rate of g is smaller than that of f. Statement II: The class of all decision problems decided by a TM in exponential time, that is O(2k), k being a constant. In the light of the above statements, choose the most appropriate answer from the options given below. |
| i ➥ Both Statement I and Statement II are correct |
| ii ➥ Both Statement I and Statement II are incorrect |
| iii ➥ Statement I is correct but Statement II is incorrect |
| iv ➥ Statement I is incorrect but Statement II is correct |
| Best Explanation: Answer: II Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.12➡ | UGC NET JUNE 2023 |
| Best Explanation: Answer: C Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.13➡ | NET December 2022 The Transition function ‘δ’ in multi-tape Turing machine is defined as : |
| i ➥ δ : 2Q × Γk → 2Q × Γk × {L, R, S}k |
| ii ➥ δ : Q × Q × Γk → Q × Q × Γk × {L, R, S} k |
| iii ➥ δ : Q × Γk → Q × Γk × {L, R, S} k |
| iv ➥ δ : Q × Γk × 2Q → Q × Γk × 2Q × {L, R, S} k |
| Best Explanation: Answer: (iii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.14➡ | NET December 2022 In pumping lemma for regular languages, to say a language is satisfying pumping lemma, what is the minimum length of ‘y’ if you consider the string as ‘xyz’. |
| i ➥ n |
| ii ➥ 2 |
| iii ➥ 1 |
| iv ➥ 0 |
| Best Explanation: Answer: (iii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.15➡ | NET December 2022 In the ɛ-NFA , M = ({q0, q1, q2, q3}, {a}, δ , q0, {q3} ) where ‘δ ’ is given in the transition table below, what is the minimum length of string to reach to the final state? 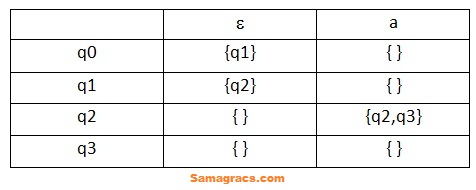 |
| i ➥ 0 |
| ii ➥ 1 |
| iii ➥ 2 |
| iv ➥ 3 |
| Best Explanation: Answer: (ii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.16➡ | NET December 2022 The Transition function ‘δ’ in mu Which of the following is /are correct about the regular expression? aa*bb*cc*dd* (A) The language for the given expression L = { anbncmdm | n≥1, m≥1 } ∪ { anbmcmdn | n≥1, m≥1 } (B) The context free language for the given expression is S→AB | C A→ aAb | ab B→ cBd | cd C→aCd | aDd D→bDc | BC (C) The language generated by this expression is equal number of a’s, followed by equal number of b’s , followed by equal number of c’s and followed by equal number of d’s. Choose the correct answer from the options given below: |
| i ➥ Only A is correct |
| ii ➥ Only B is Correct |
| iii ➥ Both A and B are correct |
| iv ➥ All the three A, B and C are correct |
| Best Explanation: Answer: (iii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.17➡ | NET December 2022 which of the following are correct on regular expression? (A) φ + L = L + φ = L (B) ɛ L = L ɛ = L (C) φ L = L φ = φ (D) φ L = L φ = L Choose the correct answer from the options given below: |
| i ➥ A, B and D only |
| ii ➥ A, B and C only |
| iii ➥ B and D only |
| iv ➥ A and D only |
| Best Explanation: Answer: (ii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.18➡ | NET December 2022 Match the following based on the language accepted by using brute force method of parsing.  Choose the correct answer from the options given below: |
| i ➥ A-(IV), B-(III), C-(I), D-(II) |
| ii ➥ A-(II), B-(IV), C-(I), D-(III) |
| iii ➥ A-(I), B-(IV), C-(III), D-(II) |
| iv ➥ A-(II), B-(III), C-(I), D-(IV) |
| Best Explanation: Answer: (ii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.19➡ | NET December 2022 What is the safest order while simplifying context Free Grammar? |
| i ➥ Elimination of ɛ-productions , Unit productions and then useless symbols & Productions. |
| ii ➥ Elimination of useless symbols & productions, ɛ- productions and then Unit Productions. |
| iii ➥ Elimination of Unit productions, ɛ- productions and then useless symbols and productions. |
| iv ➥ Elimination of ɛ- productions. Useless symbols and productions and then Unit Productions. |
| Best Explanation: Answer: (i) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.20➡ | NET December 2022 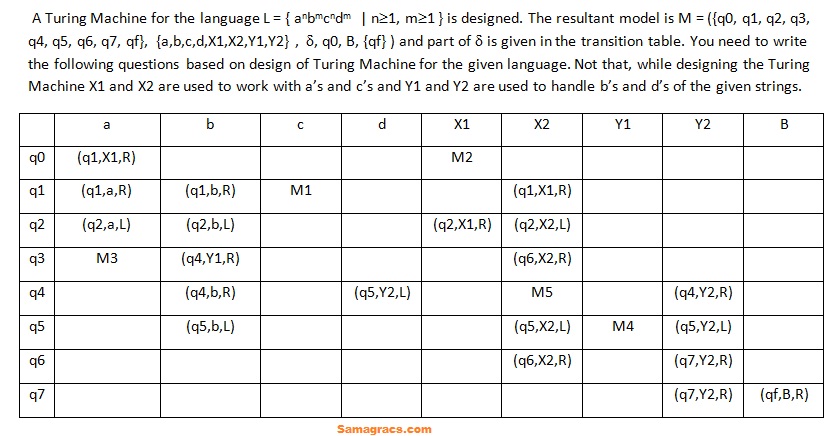 What is the Move in the cell with number ‘M1’ of the resultant Table? |
| i ➥ (q2,X2,R) |
| ii ➥ (q2,X2,L) |
| iii ➥ (q3,X2,L) |
| iv ➥ Error Entry |
| Best Explanation: Answer: (ii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.21➡ | NET December 2022 What is the Move in the cell with number ‘M2’ of the resultant Table? |
| i ➥ (q1,X1,R) |
| ii ➥ (q1,a,R) |
| iii ➥ (q2,X1,R) |
| iv ➥ Error Entry |
| Best Explanation: Answer: (iv) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.22➡ | NET December 2022 What is the Move in the cell with number ‘M3’ of the resultant Table? |
| i ➥ (q1,X1,L) |
| ii ➥ (q4,X1,R) |
| iii ➥ (q1,X1,R) |
| iv ➥ Error Entry |
| Best Explanation: Answer: (iii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.23➡ | NET December 2022 What is the Move in the cell with number ‘M4’ of the resultant Table? |
| i ➥ (q5,Y1,L) |
| ii ➥ (q3,Y1,R) |
| iii ➥ (q4,Y1,L) |
| iv ➥ (q3,Y1,L) |
| Best Explanation: Answer: Mark to All Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.24➡ | NET December 2022 What is the Move in the cell with number ‘M5’ of the resultant Table? |
| i ➥ (q4,X2,R) |
| ii ➥ (q5,X2,R) |
| iii ➥ (q5,X2,L) |
| iv ➥ Error Entry |
| Best Explanation: Answer: Mark to All Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.25➡ | NET june 2022 Consider the Properties of recursively enumerable sets: (A) Finiteness (B) Context freedom (C) Emptiness Which of the following is true? |
| i ➥ Only (A) and (B) are not decidable |
| ii ➥ Only (B) and (C) are not decidable |
| iii ➥ Only (C) and (A) are not Decidable |
| iv ➥ All (A), (B) and (C) are not decidable |
| Best Explanation: Answer: (iv) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.26➡ | NET June 2022 Consider the production rules of grammar G: S→ AbB A→ aAb/λ B→ bB/λ Which of the following language L is generated by grammar G? |
| i ➥ L={ anbm : n≥0, m>n} |
| ii ➥ L={ anbm : n≥0, m≥0} |
| iii ➥ L={ anbm : n≥m} |
| iv ➥ L={ anbm : n≥m} |
| Best Explanation: Answer: (i) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.27➡ | NET June 2022 Consider the language L= {anbm: n≥4, m≤3} Which of the following regular expression represents language L? |
| i ➥ aaaa*(λ+b+bb+bbb) |
| ii ➥ aaaaa*(b+bb+bbb) |
| iii ➥ aaaaa*(λ+b+bb+bbb) |
| iv ➥ aaaa*(b+bb+bbb) |
| Best Explanation: Answer: I Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.28➡ | NET June 202 Match List (I) with List (II): 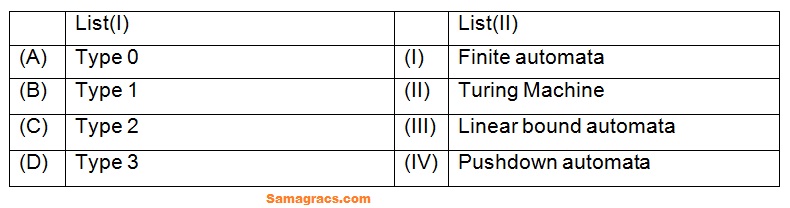 Choose the correct answer from the options given below: |
| i ➥ (A)-(III),(B)-(IV),(C)-(II),(D)-(I) |
| ii ➥ (A)-(II),(B)-(III),(C)-(IV),(D)-(I) |
| iii ➥ (A)-(III),(B)-(IV),(C)-(I),(D)-(II) |
| iv ➥ (A)-(II),(B)-(III),(C)-(I),(D)-(IV) |
| Best Explanation: Answer: (ii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.29➡ | NET June 2022 |
| i ➥ L = {a2nbn : n≥0} |
| ii ➥ L = {anb2n : n≥0} |
| iii ➥ L = {a2nbn : n>0} |
| iv ➥ L = {anb2n : n>0} |
| Best Explanation: Answer: (ii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.30➡ | NET June 2022 Consider L = {ab, aa, baa} Which of the following string is NOT in L? |
| i ➥ baaaaabaaaaa |
| ii ➥ abaabaaabaa |
| iii ➥ aaaabaaaa |
| iv ➥ baaaaabaa |
| Best Explanation: Answer: (i) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.31➡ | NET June 2022 The reduced grammar equivalent to the grammar, whose production rules are given below is S—> AB | CA B—> BC | AB A—> a C—> aB | b |
| i ➥ S—> CA , A—> a, C—> b |
| ii ➥ S—> CA | B , B—> BC | B, A—> a , C—> aB | b |
| iii ➥ S—> CA | B, B —> BC , A—> a , C—> aB | b |
| iv ➥ S—> AB | AC, B —> BC | BA, A—> a , C —> aB | b |
| Best Explanation: Answer: (i) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.32➡ | NET June 2022 |
| i ➥ Only PCP in X has solution |
| ii ➥ Only PCP in Y has solution |
| iii ➥ PCP in both X and Y has solution |
| iv ➥ PCP neither in X nor in Y has solution |
| Best Explanation: Answer: (iii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.33➡ | NET June 2022 Consider the following statements about Context Free Language ( CFL) : Statement (I) : CFL is closed under homomorphism Statement (II) : CFL is closed under complement Which of the following is correct? |
| i ➥ Statement (I) is true and statement (II) is false |
| ii ➥ Statement (II) is true and statement (I) is false |
| iii ➥ Both statement (I) and statement (II) are true |
| iv ➥ Both statement (I) and statement (II) are false |
| Best Explanation: Answer: (i) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.34➡ | NET June 2021 Which of the following languages are not regular? A. L={ (01)n0k | n > k, k>=0 } B. L={ cnbkan+k | n >= 0, k>=0 } C. L={ 0n1k | n≠k } Choose the correct answer from the options given below: |
| i ➥ A and C only |
| ii ➥ A and B only |
| iii ➥ A, B and C |
| iv ➥ B and C only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
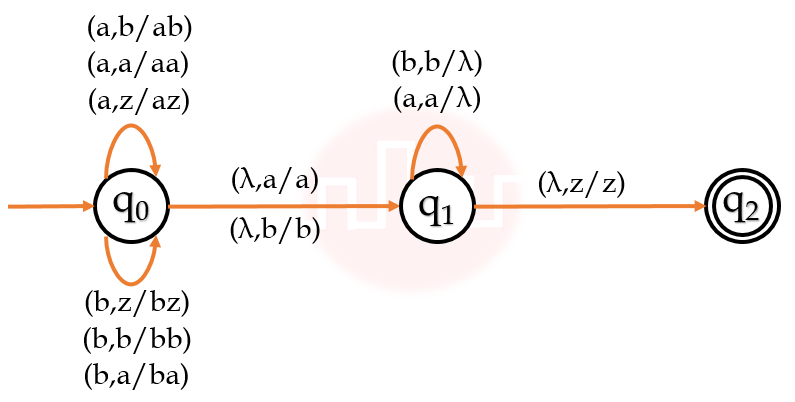
| Q.35➡ | NET June 2021 What language is accepted by the pushdown automaton M=({q0, q1, q2}, {a, b}, {a, b, z}, δ, q0, z, {q2}) with δ(q0, a, a) ={ (q0, aa) }; δ(q0, b, a) ={(q0, ba)} δ(q0, a, b) ={ (q0, ab) }; δ(q0, b, b) ={ (q0, bb) } δ(q0, a, z) ={ (q0, az) }; δ(q0, b, z) ={ (q0, bz) } δ(q0, λ, b) ={ (q1, b) }; δ(q0, λ, a) ={ (q1, a) } δ(q1, a, a) ={ (q1, λ) }; δ(q1, b, b) ={ (q1, λ) } δ(q1, λ, z) ={ (q2, z) }? |
| i ➥ L = { w | na(w) <= nb(w), w Є {a, b}+}} |
| ii ➥ L = { w | na(w) = nb(w), w Є {a, b}+}} |
| iii ➥ L = { w | nb(w) <= na(w), w Є {a, b}+}} |
| iv ➥ L= {wwR | w Є {a, b}+} |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.36➡ | NET June 2021 L1 = { 0n1n0m | n>=1, m>=1 } L2 = { 0n1m0m | n>=1, m>=1 } L3 = { 0n1n0n | n>=1} Which of the following are correct statements? A. L3 =L1 ∩ L2 B. L1 and L2 are context free languages but L3 is not a context free language C. L1 and L2 are not context free languages but L3 is a context free language D. L1 is a subset of L3 Choose the correct answer from the options given below: |
| i ➥ A and C only |
| ii ➥ A and D only |
| iii ➥ A only |
| iv ➥ A and B only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.37➡ | NET June 2021 Any string of terminals that can generated by the following context free grammar (where S is start non-terminal symbol) S→XY X→0X|1X|0 Y→Y0|Y1|0 |
| i ➥ has at least one 1 |
| ii ➥ has no consecutive 0’s or 1’s |
| iii ➥ should end with 0 |
| iv ➥ has at least two 0’s |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.38➡ | NET June 2021 Match List I with List II 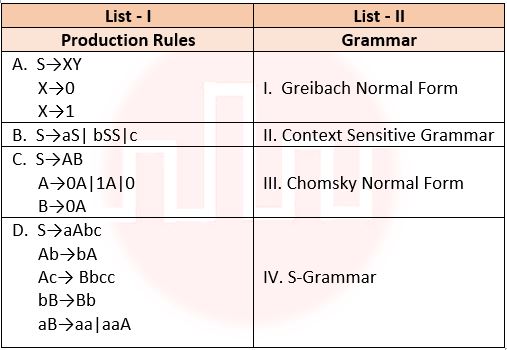 Choose the correct answer from the options below: |
| i ➥ A – III, B -I , C – IV, D – II |
| ii ➥ A – III, B -II , C – I, D – IV |
| iii ➥ A – III, B -IV, C – I, D – II |
| iv ➥ A – IV, B -III , C – I, D – II |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.39➡ | NET June 2021 What is the minimum number of states required to the finite automaton equivalent to the transition diagram given below?  |
| i ➥ 3 |
| ii ➥ 4 |
| iii ➥ 5 |
| iv ➥ 6 |
| Answer: III ➥ Click below to see detailed Solution |
| [Easy Solution] | Explanation On YouTube | Page Fault | Help-Line |
| Q.40➡ | NET June 2021 Given below are two statements Statement I: The family of context free languages is closed under homomorphism Statement II: The family of context free languages is closed under reversal. In light of the above statements, choose the correct answer from the options given below |
| i ➥ Both Statement I and Statement II are false |
| ii ➥ Both Statement I and Statement II are true |
| iii ➥ Statement I is false but Statement II is true |
| iv ➥ Statement I is true but Statement II is false |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.41➡ | NET June 2021 Find the regular expression for the language accepted by the automata given below. 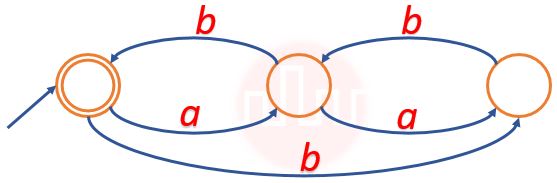 |
| i ➥ (a+b)ab(ab+bb+ aa*(a+b)ab)* |
| ii ➥ (aa*(a+b)ab)* |
| iii ➥ a*(a+b)ab(ab+bb+ aa*(a+b)ab)* |
| iv ➥ a*ab(ab+bb+ aa*(a+b)ab)* |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.42➡ | NET November 2020 Which of the following statements is true? |
| i➥ The union of two context free languages is context free. |
| ii ➥ The intersection of two context free languages is context free. |
| iii ➥ The complement of a context free language is context free. |
| iv ➥ If a language is context free, it can always be accepted by a deterministic pushdown automaton. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.43➡ | NET November 2020 Consider the following languages: 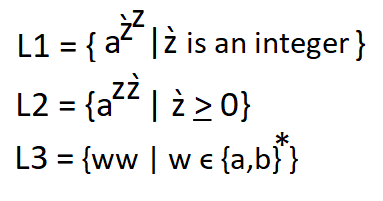 Which of the languages is (are) regular? |
| i ➥ L1 and L2 only |
| ii ➥ L1 and L3 only |
| iii ➥L1 only |
| iv ➥ None of these |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Theory of Computation Subject Wise UGC NET Question Analysis
| Q.44➡ | NET November 2020 Consider the following regular expressions: a) r=a(b+a)* b) s=a(a+b)* c) t=aa*b Choose the correct answer from the options given below based on the relation between the languages generated by the regular expressions above: |
| i ➥ L(r)⊆L(s)⊆L(t) |
| ii ➥ L(r)⊇L(s)⊇L(t) |
| iii ➥ L(r)⊇L(t)⊇L(s) |
| iv ➥ L(s)⊇L(t)⊇L(r) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.45➡ | NET November 2020 Let L1 and L2 be languages over Σ =(a,b) represented by the regular expressions (a* + b)* and (a+b)* respectively. Which of the following is true with respect to the two languages? |
| i ➥ L1 ⊂ L2 |
| ii ➥ L2 ⊂ L1 |
| iii ➥ L1 = L2 |
| iv ➥ L1 ∩ L2 = ɸ |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.46➡ | NET November 2020 Which of the following grammars is (are) ambiguous? (A) s → ss | asb | bsa | λ (B) s → asbs | bsas | λ (C) s → aAB A → bBb B → A | λ where λ denotes empty string Choose the correct answer from the options given below: |
| i ➥ (A) and (C) only |
| ii ➥ (B) only |
| iii ➥ (B) and (C) only |
| iv ➥ (A) ,(B) and (C) only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.47➡ | NET November 2020 Match List I with List II: LR: Regular languages, LCF: Context free language, LREC: Recursive language, LRE: Recursively enumerable language.  Choose the correct answer from the options given below: |
| i ➥ A-II, B-III, C-I |
| ii ➥ A-III, B-I, C-II |
| iii ➥ A-I, B-II, C-III |
| iv ➥ A-II, B-I, C-III |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.48➡ | NET November 2020 Consider L=L1 ∩ L2 where 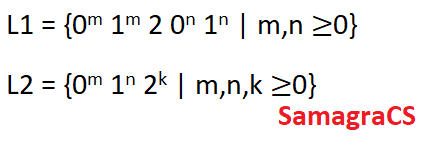 Then, the language L is |
| i ➥ Recursively enumerable but not context free |
| ii ➥ Regular |
| iii ➥ Context free but not regular |
| iv ➥ Not recursive |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.49➡ | NET November 2020 Given below are two statements: Statement I: The problem “Is L1 ∧ L2=Ø?” is undecidable for context sensitive languages L1 and L2. Statement II: The problem “Is W ∈ L?”is decidable for context sensitive language L, (where W is a string). In the light of the above statements, choose the correct answer from the options given below: |
| i ➥ Both Statement I and Statement II are true |
| ii ➥ Both Statement I and Statement II are false |
| iii ➥ Statement I is correct but Statement II is false |
| iv ➥ Statement I is incorrect but Statement II is true |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.50➡ | NET November 2020 Let G1 and G2 be arbitrary context free languages and R an arbitrary regular language. Consider the following problems: A) Is L(G1)=L(G2)? B) Is L(G2)≤L(G1)? C) Is L(G1)=R? Which of the problems are undecidable? Choose the correct answer from the options given below: |
| i ➥ (A) only |
| ii ➥ (B) only |
| iii ➥ (A) and (B) only |
| iv ➥ (A), (B) and (C) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Theory of Computation Subject Wise UGC NET Question Analysis
| Q.51➡ | NET December 2019 Let G = (V, T, S, P) be any context-free grammar without any λ-productions or unit productions. Let K be the maximum number of symbols on the right of any production P. The maximum number of production rules for any equivalent grammar in Chomsky normal form is given by: |
| i ➥ (K – 1) |P| + |T| – 1 |
| ii ➥ (K – 1) |P| +| T| |
| iii ➥ K |P| + |T| – 1 |
| iv ➥ K |P| + |T| |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.52➡ | NET December 2019 Consider the following languages:  Which one of the following is (are) inherently ambiguous language(s)? |
| i ➥ Only L1 |
| ii ➥ Only L2 |
| iii ➥ Both L1 and L2 |
| iv ➥ Neither L1 nor L2 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.53➡ | NET December 2019 Consider Σ = {w, x} and T = {x, y, z}. Define homomorphism h by : h(x) = xzy h(w) = zxyy If L is the regular language denoted by r=(w+x*)(ww)*. then the regular language h(L) is given by |
| i ➥ (z x yy + xy) (z x yy) |
| ii ➥ (zxyy + (xzy)* (zxyy zxyy)* |
| iii ➥ (zxyy + xyz) (zxyy)* |
| iv ➥ (zxyy + (xzy)* (zxyy zxyy) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.54➡ | NET December 2019 Consider the following statements: S1: These exists no algorithm for deciding if any two Turning machine M1 and M2 accept the same language. S2: Let M1 and M2 be arbitrary Turing machines. The problem to determine L(M1)⊆ L(M2)is undecidable. Which of the statements is (are) correct? |
| i ➥ Only S1 |
| ii ➥ Only S2 |
| iii ➥ Both S1 and S2 |
| iv ➥ Neither S1 nor S1 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.55➡ | NET December 2019 Consider the following grammar : S→0A|0BB A→00A| λ B→1B|11C C→B Which language does this grammar generate? |
| i ➥ L((00) * 0+(11)*1) |
| ii ➥ L(0(11)* + 1(00)*) |
| iii ➥ L((00)*0) |
| iv ➥ L(0(11) *1) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.56➡ | NET December 2019 Let A = (001, 0011, 11, 101} and B = (01, 111, 111, 010}. Similarly, let C = {00, 001, 1000} and D = {0, 11,011}. Which of the following pairs have a post-correspondence solution? |
| i ➥ Only pair (A, B) |
| ii ➥ Only pair (C, D) |
| iii ➥ Both (A, B) and (C, D) |
| iv ➥ Neither (A, B) nor (C, D) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.57➡ | NET December 2019 Consider the language L={n>2} on Σ={a,b}. Which one of the following generates the language L? |
| i ➥ S →aA |a,A → aAb |b |
| ii ➥ S → aaA |λ, A → aAb|λ |
| iii ➥ S → aaaA |a, A → aAb|λ |
| iv ➥ S → aaaA , A → aAb|λ |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.58➡ | NET December 2019 Consider the following statements with respect to the language L = {anbn | n ≥ 0}  Which one of the following is correct? |
| i ➥ Only S1 and S2 |
| ii ➥ Only S1 and S3 |
| iii ➥ Only S2 and S3 |
| iv ➥ S1, S2 and S3 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.59➡ | NET June 2019 Which of the following problems is/are decidable problem(s) (recursively enumerable) on a Turing machine M? (a) G is a CFG with L(G)=∅ (b) There exist two TMs M1 and M2 such that L(M) ⊆{L(M1)UL(M2)}= language of all TMs (c) M is a TM that accepts w using a most 2|w| cells of tape |
| i ➥ (a) and (b) only |
| ii ➥ (a) only |
| iii ➥ (a), (b) and (c) |
| iv ➥ (c) only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.60➡ | NET June 2019 For a statement A language L ⊆ Σ* is recursive if there exists some Turing machine M Which of the following conditions is satisfied for any string w? |
| i ➥ If w ε L, then m accepts w and M will not halt |
| ii ➥ If w ∉ L, then M accepts w and M will halt by reaching at final state |
| iii ➥ If w ∉ L, then M halts without reaching to acceptable state |
| iv ➥ If w ε L, then M halts without reaching to an acceptable state |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.61➡ | NET June 2019 Match List-I with List-II: Where L1 : Regular language L2 : Context-free language L3 : Recursive language L4 : Recursively enumerable language 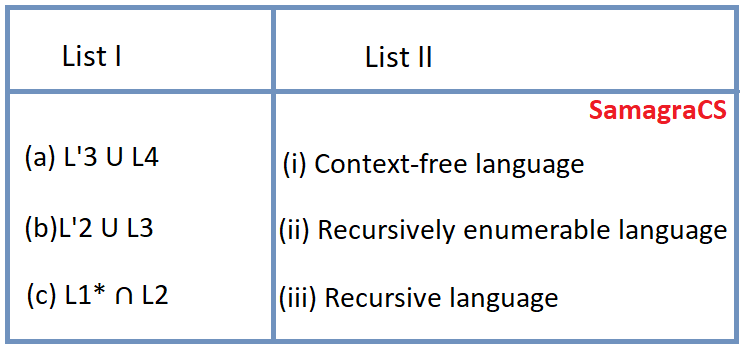 Choose the correct from those given below: |
| i ➥ (a)-(ii); (b)-(i); (c)-(iii) |
| ii ➥ (a)-(ii); (b)-(iii); (c)-(i) |
| iii ➥ (a)-(iii); (b)-(i); (c)-(ii) |
| iv ➥ (a)-(i); (b)-(ii); (c)-(iii) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.62➡ | NET June 2019 How can the decision algorithm be constructed for deciding whether context-free language L is finite? (a) By constructing redundant CFG in CNF generating language L (b) By constructing non-redundant CFG G in CNF generating language L (c) By constructing non-redundant CFG in CNF generating language L-{∧} (∧ stands for null) Which of the following is correct? |
| i ➥ (a) only |
| ii ➥ (b) only |
| iii ➥ (c) only |
| iv ➥ None of(a),(b) and (c) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.63➡ | NET June 2019 How many states are there in a minimum state automata equivalent to regular expression given below? Regular expression is a*b(a+b). |
| i ➥ 1 |
| ii ➥ 2 |
| iii ➥ 3 |
| iv ➥ 4 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.64➡ | NET June 2019 Consider the following grammar: S→ XY X→ YaY | a and y → bbX Which of the following statements is/are true about the above grammar? (a) Strings produced by the grammar can have consecutive three a’s (b) Every string produced by the grammar have alternate a and b (c) Every string produced by the grammar have at least two a’s (d) Every string produced by the grammar have b’s in multiple of 2. |
| i ➥ (a) only |
| ii ➥ (b) and (c) only |
| iii ➥ (d) only |
| iv ➥ (c) and (d) only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.65➡ | NET December 2018 Consider the following two languages: L 1 = {X| for some y with | Y| = 2 |X| , XY∈ L and L is regular language} L 2 = { X | for some y such that |X| = |Y|, XY∈ L and L is regular language} Which one of the following is correct? |
| i ➥ Both L 1 and L 2 are regular languages |
| ii ➥ Both L 1 and L 2 are not regular languages |
| iii ➥ Only L 1 is regular language |
| iv ➥ Only L 2 is regular language |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.66➡ | NET December 2018 Consider the following language: L 1 = { an+m bn am | n, m ≥ 0 } L 2 = { an+m bn+m an+m |n, m ≥ 0 } Which one of the following is correct? |
| i ➥ Only L 1 is Context Free Language |
| ii ➥ Both L 1 and L 2 are not Context Free Language |
| iii ➥ Only L 1 is Context Free Language |
| iv ➥ Both L 1 and L 2 are Context Free Language |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.67➡ | NET December 2018 Consider the following problems: (i) Whether a finite automaton halts on all inputs? (ii) Whether a given Context Free Language is regular? (iii) Whether a Turing Machine computes the product of two numbers? Which one of the following is correct? |
| i ➥ Only (ii) and (iii) are undecidable problems |
| ii ➥ (i), (ii) and (iii) are undecidable problems |
| iii ➥ Only (i) and (ii) are undecidable problems |
| iv ➥ Only (i) and (iii) are undecidable problems |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.68➡ | NET December 2018 Consider the language L given by L = { 2nk | k > 0 , and n is non−negative integer number } The minimum number of states of finite automaton which accept the language L is |
| i ➥ n |
| ii ➥ n+1 |
| iii ➥ 2n |
| iv ➥ n (n + 1 )/2 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.69➡ | NET December 2018 Which of the following problem is decidable for recursive language (L) ? |
| i ➥ Is L = ф ? |
| ii ➥ Is w∈L, where w is a string ? |
| iii ➥ Is L=R, where R is given regular set ? |
| iv ➥ Is L = Σ* ? |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.70➡ | NET December 2018 Consider R to be any regular language and L1, L2 be any two context-free languages Which one of the following is correct ? A. (L1 ⋃ L2 ) − R is context free B. L’1 is context free C. L1 − R is context free D. L1 ⋂ L2 is context free |
| i ➥ A, B and D only |
| ii ➥ A and C only |
| iii ➥ B and D only |
| iv ➥ A only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.71➡ | NET June 2018 Two finite state machines are said to be equivalent if they : |
| i ➥ Have the same number of edges |
| ii ➥ Have the same number of states |
| iii ➥ Recognize the same set of tokens |
| iv ➥ Have the same number of states and edges |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.72➡ | NET June 2018 The finite state machine given in figure below recognizes: 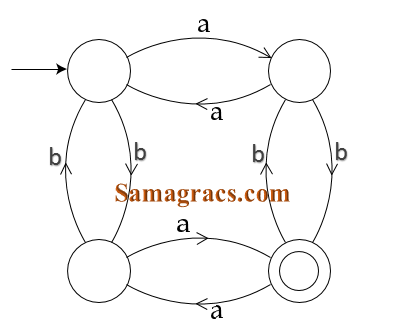 |
| i ➥ Any string of odd number of a’s |
| ii ➥ Any string of odd number of b’s |
| iii ➥ Any string of even number of a’s and odd number of b’s |
| iv ➥ Any string of odd number of a’s and odd number of b’s |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.73➡ | NET June 2018 A pushdown automata behaves like a Turing machine when the number of auxiliary memory is: |
| i ➥ 0 |
| ii ➥ 1 |
| iii ➥ 1 or more |
| iv ➥ 1 or more |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.74➡ | NET June 2018 Pushdown automata can recognize language generated by : |
| i ➥ Only context free grammar |
| ii ➥ Only regular grammar |
| iii ➥ Context free grammar or regular grammar |
| iv ➥ Only context sensitive grammar |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.75➡ | NET June 2018 To obtain a string of n Terminals from a given Chomsky normal form grammar, the number of productions to be used is: |
| i ➥ 2n−1 |
| ii ➥ 2n |
| iii ➥ n+1 |
| iv ➥ n2 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.76➡ | NET June 2018 Context sensitive language can be recognized by a: |
| i ➥ Finite state machine |
| ii ➥ Deterministic finite automata |
| iii ➥ Non-deterministic finite automata |
| iv ➥ Linear bounded automata |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.77➡ | NET June 2018 The set A={ 0n 1n 2n | n=1, 2, 3, ……… } is an example of a grammar that is : |
| i ➥ Context sensitive |
| ii ➥ Context free |
| iii ➥ Regular |
| iv ➥ None of the above |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.78➡ | NET November 2017 Paper III The logic of pumping lemma is an example of______________. |
| i ➥ Iteration |
| ii ➥ Recursion |
| iii ➥ The divide and conquer principle |
| iv ➥ The pigeonhole principle |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.79➡ | NET November 2017 Paper III Pumping lemma for regular language is generally used for proving: |
| i ➥ Whether two given regular expressions are equivalent |
| ii ➥ A given grammar is ambiguous |
| iii ➥ A given grammar is regular |
| iv ➥ A given grammar is not regular |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.80➡ | NET November 2017 Paper III Which of the following problems is undecidable? |
| i ➥ To determine if two finite automata are equivalent |
| ii ➥ Membership problem for context free grammar |
| iii ➥ Finiteness problem for finite automata |
| iv ➥ Ambiguity problem for context free grammar |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.81➡ | NET November 2017 Paper III Finite state machine can recognize language generated by__________. |
| i ➥ Only context free grammar |
| ii ➥ Only context sensitive grammar |
| iii ➥ Only regular grammar |
| iv ➥ any unambiguous grammar |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.82➡ | NET November 2017 Paper III The language L = {ai b ci │ i >= 0} over the alphabet {a, b, c} is: |
| i ➥ A regular language. |
| ii ➥ Not a deterministic context free language but a context free language. |
| iii ➥ Recursive and is a deterministic context free language. |
| iv ➥ Not recursive. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.83➡ | NET November 2017 Paper III Which of the following statements is not correct? |
| i ➥ Every recursive language is recursively enumerable. |
| ii ➥ L = {0n1n 0n │n=1, 2 , 3, ….} is recursively enumerable. |
| iii ➥ Recursive languages are closed under intersection. |
| iv ➥ Recursive languages are not closed under intersection. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.84➡ | NET November 2017 Paper III Context free grammar is not closed under: |
| i ➥ Concatenation |
| ii ➥ Complementation |
| iii ➥ Kleene Star |
| iv ➥ Union |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.85➡ | NET November 2017 Paper III Consider the following languages: L1 = {am bn │ m ≠ n} L2 = {am bn │ m = 2n+1} L3 = {am bn │ m ≠ 2n} Which one of the following statement is correct ? |
| i ➥ Only L1 and L2 are context free languages |
| ii ➥ Only L1 and L3 are context free languages |
| iii ➥ Only L2 and L3 are context free languages |
| iv ➥ L1, L2 and L3 are context free languages |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.86➡ | NET January 2017 Paper II Which of the following strings would match the regular expression : p+ [3 – 5]∗ [xyz]? I. p443y II. p6y III. 3xyz IV. p35z V. p353535x VI. ppp5 |
| i ➥ I, III and VI only |
| ii ➥ IV, V and VI only |
| iii ➥ II, IV and V only |
| iv ➥ I, IV and V only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.87➡ | NET January 2017 Paper III Which of the following are not regular? (A) Strings of even number of a’s. (B) Strings of a’s, whose length is a prime number. (C) Set of all palindromes made up of a’s and b’s. (D) Strings of a’s whose length is a perfect square. |
| i ➥ (A) and (B) only |
| ii ➥ (A), (B) and (C) only |
| iii ➥ (B), (C) and (D) only |
| iv ➥ (B) and (D) only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.88➡ | NET January 2017 Paper III Consider the languages L1 = φ and L2 = {1}. Which one of the following represents L1* ∪ L1L2 ? |
| i ➥ {∈} |
| ii ➥ {∈, 1} |
| iii ➥ Φ |
| iv ➥ 1* |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.89➡ | NET January 2017 Paper III Given the following statements : (A) A class of languages that is closed under union and complementation has to be closed under intersection. (B) A class of languages that is closed under union and intersection has to be closed under complementation. Which of the following options is correct? |
| i ➥ Both (A) and (B) are false. |
| ii ➥ Both (A) and (B) are true. |
| iii ➥ (A) is true, (B) is false. |
| iv ➥ (A) is false, (B) is true. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.90➡ | NET January 2017 Paper III Let G = (V, T, S, P) be a context-free grammar such that every one of its productions is of the form A → v, with |v| = K > 1. The derivation tree for any W ∈ L(G) has a height h such that |
| i ➥ logK|W| ≤ h ≤ logK((|W|-1) / k-1) |
| ii ➥ logK|W| ≤ h ≤ logK(K|W|) |
| iii ➥ logK|W| ≤ h ≤ K logK|W| |
| iv ➥ logK|W| ≤ h ≤ ((|W|-1) / k-1) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.91➡ | NET January 2017 Paper III Given the following two languages: L1= {an bn | n ≥ 0, n ≠ 100} L2 = {w ∈ {a, b, c}*| na(w) = nb(w) = nc(w)} Which of the following options is correct ? |
| i ➥ Both L1 and L2 are not context free language |
| ii ➥ Both L1 and L2 are context free language. |
| iii ➥ L1 is context free language, L2 is not context free language. |
| iv ➥ L1 is not context free language, L2 is context free language. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.92➡ | NET January 2017 Paper III Given the following two statements : A. L = {w|na(w) = nb(w)} is deterministic context free language, but not linear. B. L = {an bn} ∪ {an b2n} is linear, but not deterministic context free language. Which of the following options is correct ? |
| i ➥ Both (A) and (B) are false. |
| ii ➥ Both (A) and (B) are true. |
| iii ➥ (A) is true, (B) is false. |
| iv ➥ (A) is false, (B) is true. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.93➡ | NET January 2017 Paper III Which of the following pairs have different expressive power? |
| i ➥ Single-tape-turing machine and multi-dimensional turing machine. |
| ii ➥ Multi-tape turing machine and multi-dimensional turing machine. |
| iii ➥ Deterministic pushdown automata and non-deterministic pushdown automata. |
| iv ➥ Deterministic finite automata and Non-deterministic finite automata |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.94➡ | NTA UGC NET January 2017 Paper III Which of the following statements is false? |
| i ➥ Every context-sensitive language is recursive. |
| ii ➥ Multi-tape turing machine and multi-dimensional turing machine. |
| iii ➥ The family of recursively enumerable languages is closed under union. |
| iv ➥ The families of recursively enumerable and recursive languages are closed under reversal. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.95➡ | NET June 2016 Paper II The number of strings of length 4 that are generated by the regular expression (0|∈)1+ 2* (3|∈), where | is an alternation character, {+, *} are quantification characters, and ∈ is the null string, is : |
| i ➥ 08 |
| ii ➥ 10 |
| iii ➥ 11 |
| iv ➥ 12 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.96➡ | NET June 2016 Paper III Let Σ = {a, b} and language L = {aa, bb}. Then, the complement of L is |
| i ➥ {λ, a, b, ab, ba} ∪ {w∈{a, b}* | |w| > 3} |
| ii ➥ {a, b, ab, ba} ∪ {w∈{a, b}* | |w| > 3} |
| iii ➥ {w ∈ { a, b}* | |w| > 3} ∪ {a, b, ab, ba} |
| iv ➥ {λ, a, b, ab, ba} ∪ {w ∈ {a, b}* | |w| ≥ 3} |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.97➡ | NET June 2016 Paper III Consider the following identities for regular expressions: (a) (r + s)* = (s + r)* (b) (r*)* = r* (c) (r* s*)* = (r + s)* Which of the above identities are true? |
| i ➥ (a) and (b) only |
| ii ➥ (b) and (c) only |
| iii ➥ (c) and (a) only |
| iv ➥ (a), (b) and (c) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.98➡ | NET June 2016 Paper III Given the following two languages : L1 = {uwwRν | u, v, w ∈ {a, b}+} L2 = {uwwRν | u, ν, w ∈ {a, b}+, |u| > |ν|} Which of the following is correct ? |
| i ➥ L1 is regular language and L2 is not regular language. |
| ii ➥ L1 is not regular language and L2 is regular language. |
| iii ➥ Both L1 and L2 are regular languages. |
| iv ➥ Both L1 and L2 are not regular languages |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.99➡ | NET June 2016 Paper III Given a Turing Machine M = ({q0 , q1 }, {0, 1}, {0, 1, B}, δ, B, {q1 }) Where δ is a transition function defined as δ(q0 , 0) = (q0 , 0, R) δ(q0 , B) = (q1 , B, R) The language L(M) accepted by Turing machine is given as : |
| i ➥ 0* 1* |
| ii ➥ 00* |
| iii ➥ 10* |
| iv ➥ 1*0* |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.100➡ | NET June 2016 Paper III Let G = (V, T, S, P) be a context-free grammar such that every one of its productions is of the form A → ν, with |ν| = k > 1. The derivation tree for any string W ∈ L (G) has a height such that |
| i ➥ h<((|W| – 1)/k-1) |
| ii ➥ logk|W| < h |
| iii ➥ logk|W| < h < ((|W| – 1)/k-1) |
| iv ➥ logk|W| <= h <= ((|W| – 1)/k-1) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.101➡ | NET August 2016 Paper II Which of the following is FALSE? |
| i ➥ The grammar S→aS|aSbS|∈, where S is the only non-terminal symbol, and ∈ is the null string, is ambiguous. |
| ii ➥ An unambiguous grammar has same leftmost and rightmost derivation. |
| iii ➥ An ambiguous grammar can never be LR(k) for any k. |
| iv ➥ Recursive descent parser is a top-down parser |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.102➡ | NET August 2016 Paper III The regular expression for the complement of the language L = {anbm|n ≥ 4, m ≤ 3} is: |
| i ➥ (λ + a + aa + aaa) b* + a* bbbb* + (a + b)* ba(a + b)* |
| ii ➥ (λ + a + aa + aaa) b* + a* bbbbb* + (a + b)* ab(a + b)* |
| iii ➥ (λ + a + aa + aaa) + a* bbbbb* + (a + b)* ab(a + b)* |
| iv ➥ (λ + a + aa + aaa)b* + a* bbbbb* + (a + b)* ba(a + b)* |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.103➡ | NET August 2016 Paper III Consider the following two languages : L1 = {0i1j| gcd (i, j) = 1} L2 is any subset of 0*. Which of the following is correct ? |
| i ➥ L1 is regular and L2* is not regular |
| ii ➥ L1 is not regular and L2* is regular |
| iii ➥ Both L1 and L2* are regular languages |
| iv ➥ Both L1 and L2* are not regular languages |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.104➡ | NET August 2016 Paper III Let L be the language generated by regular expression 0*10* and accepted by the deterministic finite automata M. Consider the relation RM defined by M. As all states are reachable from the start state, RM has____equivalence classes. |
| i ➥ 2 |
| ii ➥ 4 |
| iii ➥ 5 |
| iv ➥ 6 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.105➡ | NET August 2016 Paper III Let L = {0n1n|n ≥ 0} be a context free language. Which of the following is correct ? |
| i ➥ L’ is context free and Lk is not context free for any k ≥ 1 |
| ii ➥ L’ is not context free and Lk is not context free for any k ≥ 1 |
| iii ➥ Both L’ and Lk is for any k ≥ 1 are context free |
| iv ➥ Both L’ and Lk is for any k ≥ 1 are not context free |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.106➡ | NET August 2016 Paper III Given a Turing Machine M = ({q0, q1, q2, q3}, {a, b}, {a, b, B}, δ, B, {q3}) Where δ is a transition function defined as δ( q0 , a) = ( q1 , a, R) δ( q1 , b) = ( q2 , b, R) δ( q2 , a) = ( q2 , a, R) δ( q3 , b) = ( q3, b, R) The language L(M) accepted by the Turing Machine is given as: |
| i ➥ aa*b |
| ii ➥ Abab |
| iii ➥ aba*b |
| iv ➥ aba* |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.107➡ | NET December 2015 Paper III The family of context sensitive languages is___________under union and______under reversal. |
| i ➥ closed, not closed |
| ii ➥ not closed, not closed |
| iii ➥ closed, closed |
| iv ➥ not closed, closed |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.108➡ | NET December 2015 Paper III Match the following: 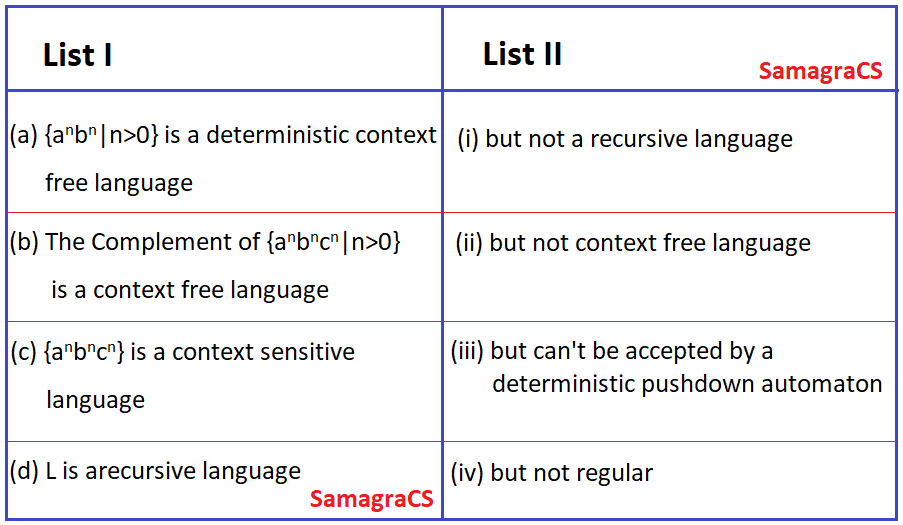 |
| i ➥ (a)-(i), (b)-(ii), (c)-(iii), (d)-(iv) |
| ii ➥ (a)-(i), (b)-(ii), (c)-(iv), (d)-(iii) |
| iii ➥ (a)-(iv), (b)-(iii), (c)-(ii), (d)-(i) |
| iv ➥ (a)-(iv), (b)-(iii), (c)-(i), (d)-(ii) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.109➡ | NET December 2015 Paper III The language of all non-null strings of a’s can be defined by a context free grammar as follows: S → aS|Sa|a The word a3 can be generated by _________different trees. |
| i ➥ Two |
| ii ➥ Three |
| iii ➥ Four |
| iv ➥ Five |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.110➡ | NET December 2015 Paper III The context free grammar given by S → XYX X → aX|bX|λ Y → bbb generates the language which is defined by regular expression: |
| i ➥ (a + b)*bbb |
| ii ➥ abbb(a + b)* |
| iii ➥ (a + b)*(bbb)(a + b)* |
| iv ➥ (a + b)(bbb)(a + b)* |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.111➡ | NET December 2015 Paper III There are exactly __ different finite automata with three states x, y and z over the alphabet {a, b} where x is always the start state. |
| i ➥ 64 |
| ii ➥ 56 |
| iii ➥ 1024 |
| iv ➥ 5832 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.112➡ | NET December 2015 Paper III Given the following two languages: L1 = {an b an |n > 0} L2 = {an b an bn + 1|n > 0} Which of the following is correct ? |
| i ➥ L1 is context free language and L2 is not context free language |
| ii ➥ L1 is not context free language and L2 is context free language |
| iii ➥ Both L1 and L2 are context free languages |
| iv ➥ Both L1 and L2 are not context free languages |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.113➡ | NET December 2015 Paper III Consider a language A defined over the alphabet Σ={0, 1} as A={0⌊n/2⌋1n :n>=0}. The expression ⌊n/2⌋ means the floor of n/2, or what you get by rounding n/2 down to the nearest integer. Which of the following is not an example of a string in A? |
| i ➥ 011 |
| ii ➥ 0111 |
| iii ➥ 0011 |
| iv ➥ 001111 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.114➡ | NET JUNE 2015 Paper III Minimal deterministic finite automaton for the language L = {0n | n ≥ 0, n ≠ 4} will have: |
| i ➥ 1 final state among 5 states |
| ii ➥ 4 final states among 5 states |
| iii ➥ 1 final state among 6 states |
| iv ➥ 5 final states among 6 states |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.115➡ | NET JUNE 2015 Paper III The regular expression corresponding to the language L where L = { x ε {0, 1}*|x ends with 1 and does not contain substring 00 } is: |
| i ➥ (1 + 01) * (10 + 01) |
| ii ➥ (1 + 01) * 01 |
| iii ➥ (1 + 01) * (1 + 01) |
| iv ➥ (10 + 01) * 01 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.116➡ | NET JUNE 2015 Paper III  |
| i ➥ q0 and q0 respectively |
| ii ➥ q0 and q1 respectively |
| iii ➥ q0 and q2 respectively |
| iv ➥ q0 and q3 respectively |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.117➡ | NET JUNE 2015 Paper III A context free grammar for L = { w | n0 ( w ) > n 1 ( w ) } is given by: |
| i ➥ S → 0 | 0 S | 1 S S |
| ii ➥ S → 0 S | 1 S | 0 S S | 1 S S | 0 | 1 |
| iii ➥ S → 0 | 0 S | 1 S S | S 1 S | S S 1 |
| iv ➥ S → 0 S |1 S | 0 | 1 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.118➡ | NET JUNE 2015 Paper III Given the following two statements: S1 : If L1 and L2 are recursively enumerable languages over ∑ , then L1 ∪ L2 and L2 ∩ L2 are also recursively enumerable. S2 : The set of recursively enumerable languages is countable. Which of the following is correct ? |
| i ➥ S1 is correct and S2 is not correct |
| ii ➥ S1 is not correct and S2 is correct |
| iii ➥ Both S1 and S2 are not correct. |
| iv ➥ Both S1 and S2 are not correct. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.119➡ | NET JUNE 2015 Paper III Given the following grammars: G1 : S → AB|aaB A → aA | ∈ B → bB | ∈ G2: S → A|B A → aAb | ab B → abB | ∈ Which of the following is correct? |
| i ➥ G1 is ambiguous and G2 is unambiguous grammars |
| ii ➥ G1 is unambiguous and G2 is ambiguous grammars |
| iii ➥ both G1 and G2 are ambiguous grammars |
| iv ➥ both G1 and G2 are unambiguous grammars |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q120➡ | NET Dec 2014 Paper III Given two languages : L1 = {(ab)n ak | n > k, k ≥ 0} L2 = {an bm | n ≠ m} Using pumping lemma for regular language, it can be shown that |
| i ➥ L1 is regular and L2 is not regular |
| ii ➥ L1 is not regular and L2 is regular |
| iii ➥ L1 is regular and L2 is regular |
| iv ➥ L1 is not regular and L2 is not regular |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.121➡ | NET Dec 2014 Paper III Regular expression for the complement of language L = {an bm | n ≥ 4, m ≤ 3} is |
| i ➥ (a + b)* ba(a + b)* |
| ii ➥ a* bbbbb* |
| iii ➥ (λ+a+aa+aaa)b∗+(a+b)∗ba(a+b)∗ |
| iv ➥ None of the above |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.122➡ | NET Dec 2014 Paper III Given the recursively enumerable language (LRE), the context sensitive language (LCS), the recursive language (LREC), the context free language (LCF) and deterministic context free language (LDCF). The relationship between these families is given by |
| i ➥ LCF ⊆ LDCF ⊆ LCS ⊆ LRE ⊆ LREC |
| ii ➥ LCF ⊆ LDCF ⊆ LCS ⊆ LREC ⊆ LRE |
| iii ➥ LDCF ⊆ LCF ⊆ LCS ⊆ LRE ⊆ LREC |
| iv ➥ LDCF ⊆ LCF ⊆ LCS ⊆ LREC ⊆ LRE |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.123➡ | NET Dec 2014 Paper III 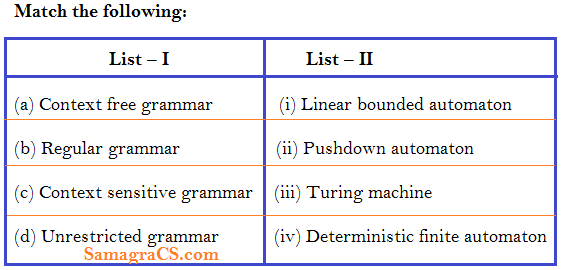 |
| i ➥ a-ii, b-iv, c-iii, d-i |
| ii ➥ a-ii, b-iv, c-i, d-iii |
| iii ➥ a-iv, b-i, c-ii, d-iii |
| iv ➥ a-i, b-iv, c-iii, d-ii |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.124➡ | NET Dec 2014 Paper III According to pumping lemma for context free languages : Let L be an infinite context free language, then there exists some positive integer m such that any w ∈ L with | w | ≥ m can be decomposed as w = u v x y z |
| i ➥ with | vxy | ≤ m such that uvi xyi z ∈ L for all i = 0, 1, 2 |
| ii ➥ with | vxy | ≤ m, and | vy | ≥ 1, such that uvi xyi z ∈ L for all i = 0, 1, 2, ……. |
| iii ➥ with | vxy | ≥ m, and | vy | ≤ 1, such that uvi xyi z ∈ L for all i = 0, 1, 2, ……. |
| iv ➥ with | vxy | ≥ m, and | vy | ≥ 1, such that uvi xyi z ∈ L for all i = 0, 1, 2, ……. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.125➡ | NET JUNE 2014 Paper II The context free grammar for the language L = {anbmck | k = |n – m|, n ≥ 0, m ≥ 0, k ≥ 0} is |
| i ➥ S → S1S3, S1 → aS1c | S2| λ, S2 → aS2b|λ, S3 → aS3b| S4 | λ, S4 → bS4c|λ |
| ii ➥ S → S1S3, S1→ aS1S2c | λ, S2 → aS2b|λ, S3 → aS3b| S4 |λ, S4 → bS4c|λ |
| iii ➥ S → S1|S2, S1→ aS1S2c | λ, S2 → aS2b | λ, S3 → aS3b | S4 |λ, S4 → bS4c|λ |
| iv ➥ S → S1 | S3, S1→ aS1c|S2 | λ, S2 → aS2b | λ, S3 → a S3b| S4 | λ, S4 → bS4c | λ |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q126➡ | NET JUNE 2014 Paper II The regular grammar for the language L = {w|na(w) and nb(w) are both even, w ∈ {a, b}*} is given by : (Assume, p, q, r and s are states) |
| i ➥ p → aq | br | λ, q → bs | ap r → as | bp, s → ar | bq, p and s are initial and final states. |
| ii ➥ p → aq | br, q → bs | ap r → as | bp, s → ar | bq, p and s are initial and final states. |
| iii ➥ p → aq | br | λ, q → bs | ap r → as | bp, s → ar | bq p is both initial and final states. |
| iv ➥ p → aq | br, q → bs | ap r → as | bp, s → ar | bq p is both initial and final states |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.127➡ | NET JUNE 2014 Paper III Let L be any language. Define even (W) as the strings obtained by extracting from W the letters in the even-numbered positions and even(L) = {even (W) | W ∈ L}. We define another language Chop (L) by removing the two leftmost symbols of every string in L given by Chop(L) = {W | ν W ∈ L, with | ν | = 2}. If L is regular language then |
| i ➥ even(L) is regular and Chop(L) is not regular |
| ii ➥ Both even(L) and Chop(L) are regular |
| iii ➥ even(L) is not regular and Chop(L) is regular |
| iv ➥ Both even(L) and Chop(L) are not regular |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.128➡ | NET JUNE 2014 Paper III 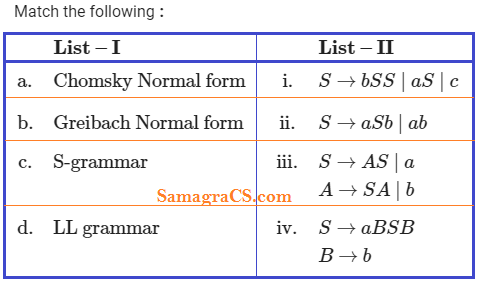 Code: |
| i ➥ a-iv, b-iii, c-i, d-ii |
| ii ➥ a-iv, b-iii, c-ii, d-i |
| iii ➥ a-iii, b-iv, c-i, d-ii |
| iv ➥ a-iii, b-iv, c-ii, d-i |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.129➡ | NET JUNE 2014 Paper III Given the following two languages : L1 = {anbn | n > 1} ∪ {a} L2 = {w C wR | w ∈ {a, b}*} Which statement is correct ? |
| i ➥ Both L1 and L2 are not deterministic. |
| ii ➥ L1 is not deterministic and L2 is deterministic |
| iii ➥ L1 is deterministic and L2 is not deterministic |
| iv ➥ Both L1 and L2 are deterministic |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |

 =1, m>=1 }”>
=1, m>=1 }”>