Discrete Structures Subject Wise UGC NET Question Analysis Part-1
Discrete Math PYQ Part-2
Q.1➡ | UGC NET DEC 2023 (A) Reflexive (B) Symmetric (C) Transitive (D) Assymmetric Choose the correct answer from the options given below : |
| i ➥ (A) and (B) Only |
| ii ➥ (B) and (C) Only |
| iii ➥ (A), (C) and (D) Only |
| iv ➥ (A), (B) and (C) Only |
| Best Explanation: Answer: (IV) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.2➡ | UGC NET DEC 2023 If universe of disclosure are all real numbers, then which of the following are true? (A) Ǝx ∀y (x+y=y) (B) ∀x ∀y(((x≥0)∧(y<0))→(x-y>0)) (C) Ǝx Ǝy(((x≤0)∧(y≤0))∧(x-y>0)) (D) ∀x ∀y((x≠0)∧(y≠0)↔(xy≠0)) Choose the correct answer from the options given below : |
| i ➥ (A) and (B) Only |
| ii ➥ (A), (C) and (D) Only |
| iii ➥ (A), (B) and (D) Only |
| iv ➥ (A), (B), (C) and (D) Only |
| Best Explanation: Answer: (IV) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.3➡ | UGC NET DEC 2023 If the universe of disclosure is set of integers, then which of the followings are TRUE? (A) ∀n ∃ m(n2 < m) (B) ∃ n ∀ m(n < m2) (C) ∃n ∀ m(nm = m) (D) ∃ n ∃m(n2 + m2 = 6) (E) 3n ∃ m(n + m = 4 ∧ n – m = 1) Choose the correct answer from the options given below : |
| i ➥ (A), (B) and (C) Only |
| ii ➥ (B) and (C) Only |
| iii ➥ (C), (D) and (E) Only |
| iv ➥ (C) and (E) Only |
| Best Explanation: Answer: (II) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.4➡ | UGC NET DEC 2023 Which of the following statement are truth statements if universe of disclosure is set of integers: (A) ∀n(n2 >= 0) (B) ∃ n(n 2 = 2) (C) ∀ n(n 2 >= n) (D) ∃ n(n2 < 0) Choose the correct answer from the options given below : |
| i ➥ (A) and (B) Only |
| ii ➥ (B) and (C) Only |
| iii ➥ (C) and (D) Only |
| iv ➥ (A) and (C) Only |
| Best Explanation: Answer: (IV) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.5➡ | UGC NET DEC 2023 Which of the following are tautology? (A) (P (P∧ Q))→(P→Q) (B) ((PQ)→Q)→(PVQ) (C) ((P V¬P)→Q)→((PV ¬P)→R) (D) (Q→(P∧ ¬P))→(R→(P∧ ¬P)) Choose the correct answer from the options given below : |
| i ➥ (A) Only |
| ii ➥ (B) Only |
| iii ➥ (A) and(B) Only |
| iv ➥ (C) and (D) Only |
| Best Explanation: Answer: (III) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.6➡ | UGC NET DEC 2023 The statement P(x): “x=x2“. If the universe of disclosure consists of integers, what are the following have truth values : (A) P(0) (B) P(1) (C) P(2) (D) Ǝx P(x) (E) ∀x P(x) Choose the correct answer from the options given below : |
| i ➥ (A), (B) and (E) Only |
| ii ➥ (A), (B) and (C) Only |
| iii ➥ (A), (B) and (D) Only |
| iv ➥ (B), (C) and (D) Only |
| Best Explanation: Answer: (IV) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.7➡ | UGC NET DEC 2023 What is the probability that a positive integer selected at random from the set of positive integer not exceeding 100 is divisible by either 2 or 5? |
| i ➥ 10/5 |
| ii ➥ 3/5 |
| iii ➥ 2/5 |
| iv ➥ 1/5 |
| Best Explanation: Answer: (II) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.8➡ | UGC NET DEC 2023 Given below are two statements: Statement (I): If H is non empty finite subset of a group G and ab∉H ∀ a, b∉H, then H is also a group Statement (II): There is no homomorphism exist from (Z, +) to (Q, +); where Z is set of integers and Q is set of rational number. In the light of the above statements, choose the most appropriate answer from the options given below: |
| i ➥ Both Statement I and Statement II are correct |
| ii ➥ Both Statement I and Statement II are incorrect |
| iii ➥ Statement I is correct but Statement II is incorrect |
| iv ➥ Statement I is incorrect but Statement II is correct |
| Best Explanation: Answer: (III) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.9➡ | UGC NET JUNE 2023 Let R = {x | x ∈ N, x is multiple of 3 and x ≤ 100} and S = {x, x ∈ N, x is a multiple of 5 and x < 100}. What is the number of elements in (R∩S) × (S∩R)? |
| i ➥ 36 |
| ii ➥ 33 |
| iii ➥ 20 |
| iv ➥ 6 |
| Best Explanation: Answer: I Explanation: Set R contains elements: (3, 6, 9, 12, 15, 18, 21, 24,….93, 96, 99) Set S contains elements: (5, 10, 15, 20, 25, 30,…85, 90, 95) R cap S = {15, 30, 45, 60, 75, 90} S cap R = {15, 30, 45, 60, 75, 90} Since the cardinality (number of elements in the sets) of both sets are 6. So (R∩S) x (S∩R) = 6*6 = 36 Option (A) is correct. |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.10➡ | UGC NET JUNE 2023 Match List I with List II List I A. A Δ B B. A−(B∪C) C. A−(B∩C) D. A∩(B−C) List II I. (A−B)∪(A−C) II. (A−B)∩(A−C) III. (A−B)∪(B−A) IV. (A∩B)−(A∩C) Choose the correct answer from the options given below: Choose the correct answer from the options given below: |
| i ➥ A-III B-II C-I D-IV |
| ii ➥ A-II B-III C-IV D-I |
| iii ➥ A-IV B-III C-I D-II |
| iv ➥ A-IV B-I C-III D-II |
| Best Explanation: Answer: I Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.11➡ | UGC NET JUNE 2023 Let N denote the set of all natural numbers and R be the relation on N*N defined by (a,b)R(c,d), if ad(b+c)=bc(a+d). Then R is |
| i ➥ Symmetric only |
| ii ➥ Reflexive only |
| iii ➥ Transitive only |
| iv ➥ An equivalence relation |
| Best Explanation: Answer: IV Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.12➡ | UGC NET JUNE 2023 Let (Z,+) denote the group of all integers under addition. Then the number of all automorphisms of (Z,+) is |
| i ➥ 1 |
| ii ➥ 2 |
| iii ➥ 3 |
| iv ➥ 4 |
| Best Explanation: Answer: II Explanation: In the case of the group of all integers under addition, (Z, +), the number of automorphisms is 2. 1.The identity function: The identity function is an automorphism that maps each integer to itself. It preserves the group’s operation and structure. 2. The negation function: The negation function is also an automorphism. It maps each integer to its additive inverse, effectively reversing the sign. This function also preserves the group’s operation and structure. These two automorphisms are the only possible automorphisms for the group (Z, +). So, the number of automorphisms of (Z, +) is 2. |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.13➡ | UGC NET JUNE 2023 If A={4n +2|n is a natural number } and B = {3n | n is a natural number }. Which of the following is correct for A ∩ B ? |
| i ➥ { 12n ^ 2 +6n|n is a natural number } |
| ii ➥ {24n 12 n is a natural number } |
| iii ➥ { 60n +30|n is a natural number } |
| iv ➥ { 12n -6|n is a natural number } |
| Best Explanation: Answer: IV Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.14➡ | UGC NET JUNE 2023 |
| i ➥ Not a homomorphism |
| ii ➥ A one-one homomorphism, which is not onto |
| iii ➥ An onto homomorphism, which is not one to one |
| iv ➥ An homomorphism |
| Best Explanation: Answer: III Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.15➡ | UGC NET JUNE 2023 Consider the following statements. A. The identity is unique in any monoid. B. A monoid is a group if there exists inverse of each element of monoid. C. Semi group has closure, associative and identity properties. D. Quasi group has closure property. Choose the correct answer from the options given below : |
| i ➥ A,B and D only |
| ii ➥ B,C and D only |
| iii ➥ A,B and C only |
| iv ➥ A,C and D only |
| Best Explanation: Answer: I Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.16➡ | NET December 2022 A relation ‘R’ is defined on ordered pairs of integers as : (x, y) R (u, v) if x<u and y>v. Then R is |
| i ➥ Neither a partial order nor an equivalence relation |
| ii ➥ A partial order but not a total order |
| iii ➥ A total order |
| iv ➥ An equivalence relation |
| Best Explanation: Answer: (i) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.17➡ | NET December 2022 Suppose you are married and you and your partner attend a party with three other married couples. Several handshakes took place. No one shook hands with himself ( or herself ) or with their partner, and no one shook hands with the same person more than once. After all hand shaking was completed , suppose you asked each person, including your partner, how many hands they had shaken. Each person gave a different answer. How many hands did your spouse shake? |
| i ➥ 1 |
| ii ➥ 2 |
| iii ➥ 3 |
| iv ➥ 4 |
| Best Explanation: Answer: (iii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.18➡ | NET December 2022 Consider the following statements: P : There exists no simple, undirected and connected graph with 80 vertices and 77 edges Q : All vertices of Euler graph are of even degree R : Every simple, undirected, connected and acyclic graph with 50 vertices has at least two vertices of degree one S : There exists a bipartite graph with more than ten vertices which is 2 – colorable. What is the number of correct statements among the above statements. |
| i ➥ 1 |
| ii ➥ 2 |
| iii ➥ 3 |
| iv ➥ 4 |
| Best Explanation: Answer: (iv) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.19➡ | NET December 2022 Q42➡ | Discrete Mathematics consider the following statements. A : There exists a Boolean algebra with 5 elements B : Every element of Boolean algebra has unique complement C : It a Lattice ‘L’ is a Boolean algebra then ‘L’ is not relatively complemented D : The direct product of two Boolean algebra is also a Boolean algebra Choose the correct answer about the four statements given above. |
| i ➥ Only A and D are correct |
| ii ➥ Only B and D are correct |
| iii ➥ All statement are NOT Correct |
| iv ➥ All statement are correct |
| Best Explanation: Answer: (ii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.20➡ | NET December 2022 Given a vector with Cartesian components (x,y) , if scaling is done with Matrix Row1[ 0.5 0 ], Row2[0 1.5] which of the following are true: (A) Decrease the vertical by three halves (B) Increase the vertical by three halves (C) Double the horizontal (D) Halves the horizontal Choose the correct from the options given below: |
| i ➥ A and C only |
| ii ➥ A and D only |
| iii ➥ B and C only |
| iv ➥ B and D only |
| Best Explanation: Answer: (iv) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.21➡ | NET December 2022 Match List (I) with List (II) 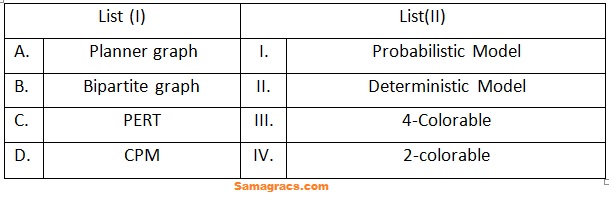 Choose the correct answer from the options given below: |
| i ➥ A-(IV), B-(III), C-(I), D-(II) |
| ii ➥ A-(III), B-(IV), C-(II), D-(I) |
| iii ➥ A-(II), B-(IV), C-(I), D-(III) |
| iv ➥ A-(III), B-(IV), C-(I), D-(II) |
| Best Explanation: Answer: (iv) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.22➡ | NET December 2022 |
| i ➥ Both statement (I) and Statement (II) are correct |
| ii ➥ Both statement (I) and Statement (II) are incorrect |
| iii ➥ Statement (I) is correct but Statement (II) is incorrect |
| iv ➥ Statement (I) is incorrect and Statement (II) is correct |
| Best Explanation: Answer: (iii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.23➡ | NET June 2022 Let ({a,b}, ) be a semigroup , where a*a = b. (A) a*a = b*a (B) b*b = b Choose the most appropriate answer from the options given below: |
| i ➥ A) only true |
| ii ➥ (B) only true |
| iii ➥ Both (A) and (B) true |
| iv ➥ Neither (A) not (B) true |
| Best Explanation: Answer: (iii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.24➡ | NET June 2022 Consider the primal problem: Maximize z = 5x1 + 12x2 + 4x3 Subject to x1 + 2x2 + x3 = 10 2x1 – x2 + 3x3 = 8 x1, x2, x3 ≥ 0 It’s dual problem is Minimize w = 10y1 + 8y2 Subject to y1 + 2y2 ≥ 5 2y1 – y2 ≥ 12 y1 + 3y2 ≥ 4 Which of the following is correct? |
| i ➥ y1≥ 0 , y2 unrestricted |
| ii ➥ y1≥ 0 , y2≥ 0 |
| iii ➥ y1 is unrestricted, y2 ≥ 0 |
| iv ➥ y1 is unrestricted, y2 is restricted |
| Best Explanation: Answer: (i) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.25➡ | NET June 2022 There are three boxes. First box has 2 white, 3 black and 4 red balls. Second box has 3 white, 2 Black and 2 red balls. Third box has 4 white, 1 black and 3 red balls. A box is chosen at random and 2 balls are drawn out of which 1 is white , and 1 is red. What is the probability that the balls came from first box? |
| i ➥ 0.237 |
| ii ➥ 0.723 |
| iii ➥ 0.18 |
| iv ➥ 0.452 |
| Best Explanation: Answer: (i) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.26➡ | NET June 2022 Let ∈ = 0.0005 and let Re be the relation { (x, y) ∈ R2 : |x-y| <∈} , Re could be interpreted as the relation approximately equal Re is (A) Reflexive (B) Symmetric (C) Transitive Choose the correct answer from the option given below : |
| i ➥ (A) and (B) only True |
| ii ➥ (B) and (C) only True |
| iii ➥ (A) and (C) only True |
| iv ➥ (A), (B) and (C) True |
| Best Explanation: Answer: (i) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
Q.27➡ | NET June 2022 |
| i ➥ X is true |
| ii ➥ Y is true |
| iii ➥ Both X and Y are True |
| iv ➥ It does not depend on X and Y |
| Best Explanation: Answer: (iii) Explanation: Upload Soon |
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.28➡ | NET June 2021 Let (X,* ) be a semi-group. Furthermore, for every a and b in X, if a ≠ b, then a*b ≠ b*a. Based on the defined semi-group, choose the correct equalities from the options given below: A. For every a in X, a*a = a B. For every a, b in X, a*b *a= a C. For every a, b, c in X, a*b *c= a*c |
| i ➥ A and B only |
| ii ➥ A and C only |
| iii ➥ A, B and C |
| iv ➥ B and C only |
| Answer: III Explanation: Given, (X,* ) be a semi-group. for every a and b in X, if a ≠ b, then a*b ≠ b*a. Concept, Semi Group(X,* ) have 2 properties, which are: 1) Closure Property if a and b in X, then a*b∈X 2) Associative Property if a,b and c in X, then (a*b)*c = a*(b*c) Let’s solve, A) For every a in X, a*a = a Lets assume a*a ≠ a Lets suppose a*a = b, where a ≠ b ⟹ a*(a*a) = a*b ⟹ (a*a)*a = a*b {∵ by associative property, a*(b*c) = (a*b)*c} ⟹ b*a = a*b {∵ we suppose a*a = b} Since it is given, for every a and b in X, if a ≠ b, then a*b ≠ b*a, but here a*b = b*a, which proves that our initial assumption is wrong. Hence, For every a in X, a*a = a (Correct) B) For every a, b in X, a*b *a= a Lets assume a*b*a ≠ a Lets suppose a*b*a = b, where a ≠ b it is given, a*b ≠ b*a, and we already suppose a*b*a = b. Now put b = a*b*a in a*b ≠ b*a ⟹ a*(a*b*a) ≠ (a*b*a)*a ⟹ (a*a)*b*a ≠ a*b*(a*a) {∵ by associative property, a*(b*c) = (a*b)*c} ⟹ a*b*a ≠ a*b*a {∵ it is given in A, a*a = a and we already proved that this is correct} Here, a*b*a ≠ a*b*a but it is actually equal, which proves that our initial assumption is wrong. Hence, For every a, b in X, a*b *a= a (Correct) C) For every a, b, c in X, a*b *c= a*c Lets assume a*b*c ≠ a*c Lets suppose a*b*c = a, and a*c=b where a ≠ b it is given, a*b ≠ b*a, and we already suppose a*b*c = a and a*c=b . Now put a= a*b*c and b = a*c in a*b ≠ b*a ⟹ (a*b*c)*(a*c) ≠ (a*c)*(a*b*c) ⟹ a*b*(c*a*c) ≠ (a*c*a)*b*c {∵ by associative property, a*(b*c) = (a*b)*c} ⟹ a*b*c ≠ a*b*c {∵ it is given in B, a*b *a= a and we already proved that this is correct. Like statement B, we can write c*a*c=c and a*c*a=a } Here, a*b*c ≠ a*b*c but it is actually equal, which proves that our initial assumption is wrong. Hence, For every a, b in X, a*b *a= a (Correct) Therefore, Option(III) is correct. |
| [Easy Solution] | Explanation On YouTube | Group | Help-Line |
| Q.29➡ | NET June 2021 How many ways are there to assign 5 different jobs to 4 different employees if every employee is assigned at least 1 job? |
| i ➥ 1024 |
| ii ➥ 20 |
| iii ➥ 240 |
| iv ➥ 625 |
| Answer: III Explanation: Given, 5 different jobs and 4 different employees every employee is assigned at least 1 job Let’s solve, Lets take 4 employees as A,B,C,D 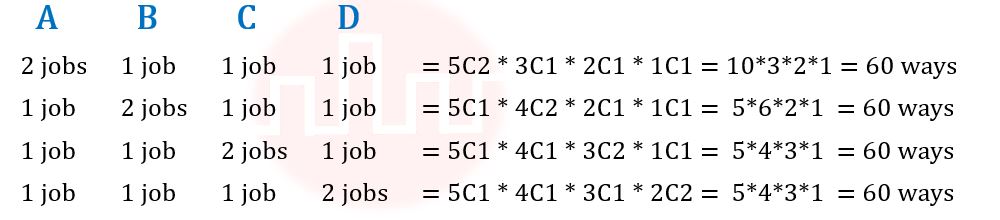 Total ways = 60 + 60 + 60 + 60 = 240 ways Therefore, Option(III) is correct. |
| [Easy Solution] | Explanation On YouTube | Permutation and Combination | Help-Line |
| Q.30➡ | NET June 2021 Consider the sentence below. There is a country that borders both India and Pakistan. Which of the following logical expressions express the above sentence correctly when the predicate Country(x) represents that x is a country and Borders(x, y) represents that the countries x and y share the border? |
| i ➥ [∃c Country(c)] ⇒ [Border (c, India) ∧ Border (c,Pakistan)] |
| ii ➥ ∃c Border (Country(c), India ∧ Pakistan) |
| iii ➥ ∃c Country(c) ∧ Border (c, India) ∧ Border (c,Pakistan) |
| iv ➥ ∃c Country(c) ⇒ [Border (c, India) ∧ Border (c,Pakistan)] |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Propositional logic | Help-Line |
| Q.31➡ | NET June 2021 Which of the following Graphs is (are) planar? 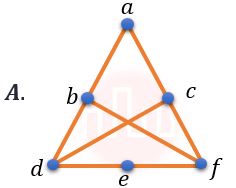 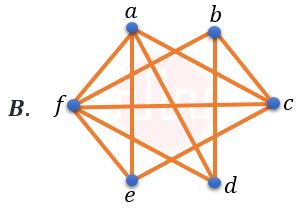 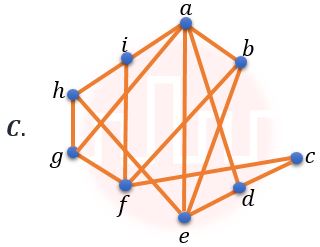 choose the correct answer from the options given below: |
| i ➥ A and B only |
| ii ➥ A only |
| iii ➥ B and C only |
| iv ➥ B only |
| More Discussion | Explanation On YouTube | Graph Theory | Help-Line |
| Q.32➡ | NET June 2021 which of the following are logically equivalent ? A. ¬p→(q→r)and q→(p∨r) B. (p→q)→r and p→(q→r) C. (p→q)→(r→s) and (p→r)→(q→s) Choose the correct answer from the options below: |
| i ➥ A and B only |
| ii ➥ A and C only |
| iii ➥ A only |
| iv ➥ B and C only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.33➡ | NET June 2021 For which value of n is Wheel graph Wn regular? |
| i ➥ 2 |
| ii ➥ 3 |
| iii ➥ 4 |
| iv ➥ 5 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.34➡ | NET June 2021 Let us assume a person climbing the stairs can take one stair or two stairs at a time. How many ways can this person climb a flight of eight stairs? |
| i ➥ 21 |
| ii ➥ 24 |
| iii ➥ 31 |
| iv ➥ 34 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
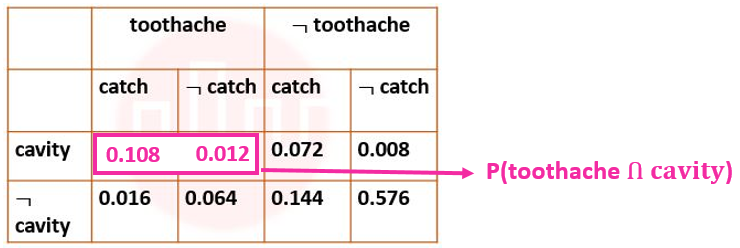
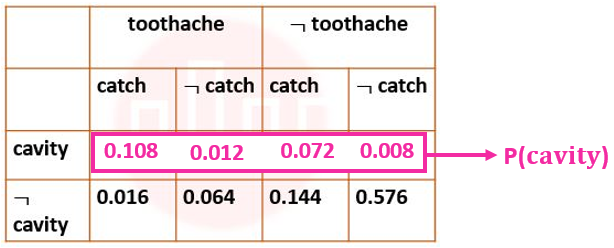
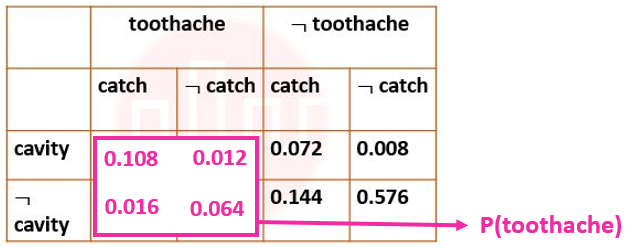
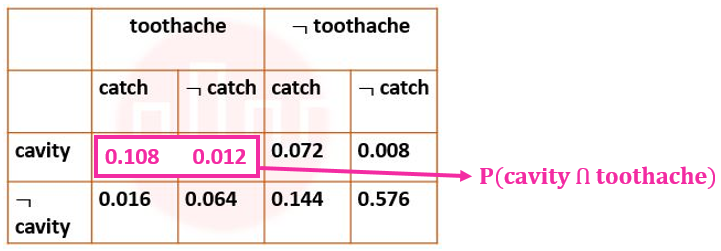
| Q.35➡ | NET June 2021 Next five questions are based on the following passage. Consider a domain consisting of three Boolean variables Toothache, Cavity, and Catch. The full joint distribution is a 2×2×2 table as shown in the figure below. 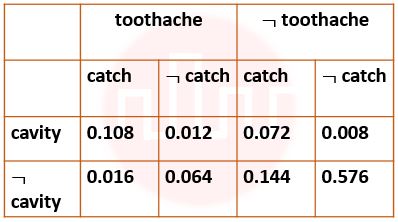 The probability of a toothache, given evidence of a cavity, P(toothache | cavity) is ____. |
| i ➥ 0.216 |
| ii ➥ 0.280 |
| iii ➥ 0.400 |
| iv ➥ 0.600 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Probability | Help-Line |
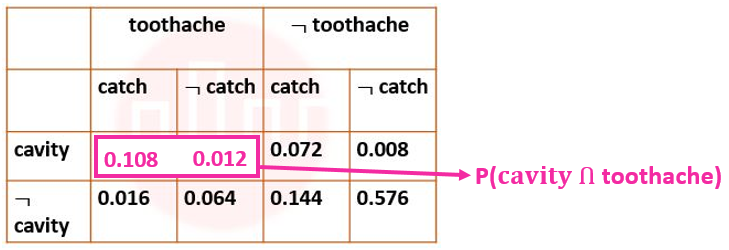
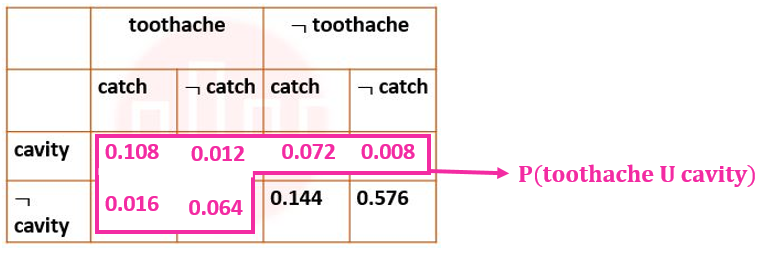
| Q.36➡ | NET June 2021 Next five questions are based on the following passage. Consider a domain consisting of three Boolean variables Toothache, Cavity, and Catch. The full joint distribution is a 2×2×2 table as shown in the figure below.  P(cavity U toothache) is________________. |
| i ➥ 0.120 |
| ii ➥ 0.200 |
| iii ➥ 0.280 |
| iv ➥ 0.600 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Probability | Help-Line |
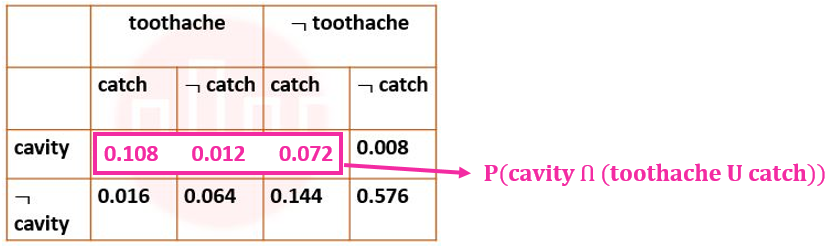
| Q.37➡ | NET June 2021 Next five questions are based on the following passage. Consider a domain consisting of three Boolean variables Toothache, Cavity, and Catch. The full joint distribution is a 2×2×2 table as shown in the figure below.  The probability for Cavity, given that either Toothache or Catch is true, P(Cavity | toothache U catch) is _______. |
| i ➥ 0.4615 |
| ii ➥ 0.5384 |
| iii ➥ 0.6000 |
| iv ➥ 0.8000 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Probability | Help-Line |
| ` Q.38➡ | NET June 2021 Next five questions are based on the following passage. Consider a domain consisting of three Boolean variables Toothache, Cavity, and Catch. The full joint distribution is a 2×2×2 table as shown in the figure below.  The marginal probability of cavity P(cavity) is _____. |
| i ➥ 0.080 |
| ii ➥ 0.120 |
| iii ➥ 0.200 |
| iv ➥ 0.216 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Probability | Help-Line |
| Q.39➡ | NET June 2021 Next five questions are based on the following passage. Consider a domain consisting of three Boolean variables Toothache, Cavity, and Catch. The full joint distribution is a 2×2×2 table as shown in the figure below.  The probability of a cavity, given evidence of a toothache, P(cavity | toothache) is ____. |
| i ➥ 0.216 |
| ii ➥ 0.280 |
| iii ➥ 0.400 |
| iv ➥ 0.600 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Probability | Help-Line |
| Q.40➡ | NET November 2020 Given below are two statements: Statement I: 5 divides n5-n whenever n is a nonnegative integer. Statement II: 6 divides n3-n whenever n is a nonnegative integer. In the light of the above statements, choose the correct answer from the options given below |
| i➥ Both Statement I and Statement II are correct |
| ii ➥ Both Statement I and Statement II are incorrect |
| iii ➥ Statement I is correct but Statement II is incorrect |
| iv ➥ Statement I is incorrect but Statement II is correct |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
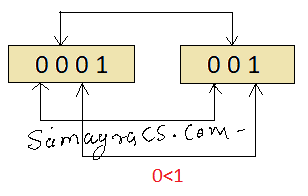
| Q.41➡ | NET November 2020 Find the lexicographic ordering of the bit strings given below based on the ordering 0 < 1. A) 001 B) 010 C) 011 D) 0001 E) 0101 Choose the correct answer from the options given below: |
| i➥ 001<010<011<0001<0101 |
| ii ➥ 0001<001<010<0101<011 |
| iii ➥ 0001<0101<001<010<011 |
| iv ➥ 001<010<0001<0101<011 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.42➡ | NET November 2020 Consider the following statements: A) Any tree is 2-colorable B) A graph G has no cycles of even length if it is bipartite C) A graph G is 2-colorable if is bipartite D) A graph G can be colored with d+1 colors if d is the maximum degree of any vertex in the graph G E) A graph G can be colored with O(log|v|) colors if it has O(|v|) edges. Choose the correct answer from the options given below: |
| i➥ (C) and (E) are incorrect |
| ii ➥ (B) and (C) are incorrect |
| iii ➥ (B) and (E) are incorrect |
| iv ➥ (A) and (D) are incorrect |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q43➡ | NET November 2020 Let) G be a directed graph whose vertex set is the set of numbers from 1 to 100. There is an edge from a vertex i to a vertex j if and only if either j=i+1 or j=3i. The minimum number of edges in a path in G from vertex 1 to vertex 100 is ___________. |
| i➥ 23 |
| ii ➥ 99 |
| iii ➥ 4 |
| iv ➥ 7 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.44➡ | NET November 2020 How many ways are there to pack six copies of the same book into four identical boxes, where a box can contain as many as six books? |
| i➥ 4 |
| ii ➥ 6 |
| iii ➥ 7 |
| iv ➥ 9 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.45➡ | NET November 2020 The number of positive integers not exceeding 100 that are either odd or the square of an integer is _. |
| i➥ 63 |
| ii ➥ 59 |
| iii ➥ 55 |
| iv ➥ 50 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.46➡ | NET December 2019 Consider the following statements: S1: If a group (G,) is of order n, and a ∈ G is such that am = e for some integer m ≤ n, then m must divide n. S2: If a group (G,) is of even order , then there must be an element and a ∈ G is such that a ≠ e and a * a = e. Which of the statements is (are) correct? |
| i➥ Only S1 |
| ii ➥ Only S2 |
| iii ➥ Both S1 and S2 |
| iv ➥ Neither S1 nor S2 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.47➡ | NET December 2019 Let a2e mod n = (ae)2 mod n and a2c+1 mod n = a (ac)2 mod n. For a = 7, b = 17 and n = 561, what is the value of ab(mod n)? |
| i➥ 160 |
| ii ➥ 166 |
| iii ➥ 157 |
| iv ➥ 67 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.48➡ | NET December 2019 Let P be the set of all people. Let R be a binary relation on P such that (a, b) is in R if a is a brother of b. Is R symmetric, transitive, an equivalence relation, a partial order relation? |
| i➥ NO.NO.NO.NO |
| ii ➥ NO.NO.YES.NO |
| iii ➥ NO.YES.NO.NO |
| iv ➥ NO.YES.YES.NO |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.49➡ | NET December 2019 What are the greatest lower bound (GLB) and the least upper bound (LUB) of the sets A = {3, 9, 12} and B = {1, 2, 4, 5, 10} if they exist in poset (z*,/)? |
| i➥ A (GLB – 3, LUB – 36); B (GLB – 1, LUB – 20) |
| ii ➥ A(GLB – 3, LUB – 12); B (GLB -1, LUB – 10) |
| iii ➥ A (GLB -1, LUB – 36); B (GLB – 2, LUB – 20) |
| iv ➥ A (GLB – 1, LUB – 12); B (GLB – 2, LUB – 10) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.50➡ | NET December 2019 A clique in an undirected graph G = (V, E) is a subset V’ ⊆ V of vertices, such that |
| i➥ If (u, v) ∈ E then u ∈ V’ and v ∈ V’ |
| ii ➥ If (u, v) ∈ E then u ∈ V’ or v ∈ V’ |
| iii ➥ Each pair of vertices in V’ is connected by an edge |
| iv ➥ All pairs of vertices in V’ are not connected by an edge |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.51➡ | NET December 2019 How many reflexive relations are there on a set with 4 elements? |
| i➥ 24 |
| ii ➥ 212 |
| iii ➥ 42 |
| iv ➥ 2 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.52➡ | NET June 2019 How many are there to place 8 indistinguishable balls into four distinguishable bins? |
| i➥ 70 |
| ii ➥ 165 |
| iii ➥ 8C4 |
| iv ➥ 8P4 T |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.53➡ | NET June 2019 Suppose that a connected planar graph has six vertices, each of degrees four. Into how many regions is the plane divided by a planar representation of this graph? |
| i➥ 6 |
| ii ➥ 8 |
| iii ➥ 12 |
| iv ➥ 10 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.54➡ | NET June 2019 The value of the derivative of the sigmoid function given by f(x)= 1 / (1+e(-2x)) at x=0 is |
| i➥ 0 |
| ii ➥ 1/2 |
| iii ➥ 1/4 |
| iv ➥ ∞ |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.55➡ | NET June 2019 Consider the poset ({3,5,9,15,24,45},|). Which of the following is correct for the given poset? |
| i➥ There exists a greatest element and a least element |
| ii ➥ There exists a greatest element but not a least element |
| iii ➥ There exists a least element but not a greatest element |
| iv ➥ There does not exist a greatest element and a least element |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.56➡ | NET June 2019 Consider the following properties with respect to a flow network G=(V,E) in which a flow is a real-valued function f:VxV→ R P1 : For all u,vεV, f(u,v)= -f(v,u) P2 : ΣvεV f(u,v)=0 for all uεV Which one of the following is/are correct? |
| i➥ Only P1 |
| ii ➥ Only P2 |
| iii ➥ Both P1 and P2 |
| iv ➥ Neither P1 nor P2 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.57➡ | NET June 2019 A web application and its support environment has not been fully fortified against attack. Web engineers estimate that the likelihood of repelihood an attack is only 30 percent. The application does not contain sensitive or controversial information, so the threat probability is 25 percent. What is the integrity of the web application? |
| i➥ 0.625 |
| ii ➥ 0.725 |
| iii ➥ 0.775 |
| iv ➥ 0.825 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.58➡ | NET June 2019 For which values of m and n does the complete bipartite graph km,n have a Hamilton circuit? |
| i➥ m≠n, m, n≥2 |
| ii ➥ m≠n, m, n≥3 |
| iii ➥ m=n, m, n≥2 |
| iv ➥ m=2, m, n≥3 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.59➡ | NET June 2019 How many cards must be selected from a standard deck of 52 cards to guarantee that at least three hearts are present among them? |
| i➥ 9 |
| ii ➥ 13 |
| iii ➥ 17 |
| iv ➥ 42 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.60➡ | NET June 2019 Find the zero-one matrix of the transitive closure of the relation given by matrix A: 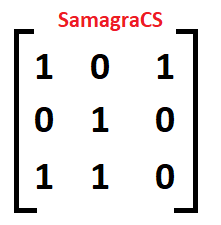 1) 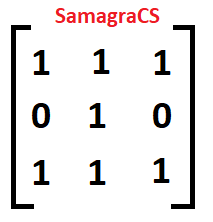 2) 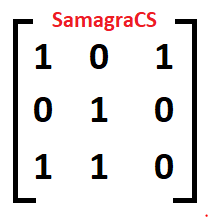 3) 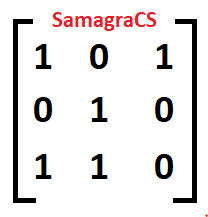 4) 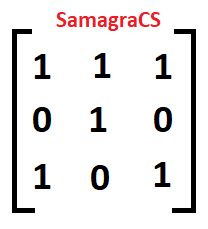 |
| i➥ 1 |
| ii ➥ 2 |
| iii ➥ 3 |
| iv ➥ 4 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.61➡ | NET June 2019 Which of the following is principal conjunctive normal form for [(pVq) ∧ ~p → ~q] ? |
| i ➥ pV~q |
| ii ➥ pVq |
| iii ➥ ~p Vq |
| iv ➥ ~p V ~q |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.62➡ | NET June 2019 Match List-I with List-II 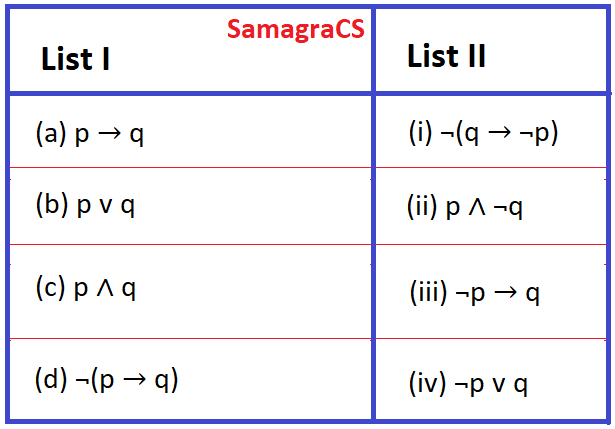 Choose the correct option from those given below: |
| i ➥ (a)-(ii);(b)-(iii);(c)-(i);(d)-(iv) |
| ii ➥ (a)-(ii);(b)-(i);(c)-(iii);(d)-(iv) |
| iii ➥ (a)-(iv);(b)-(i);(c)-(iii);(d)-(ii) |
| iv ➥ (a)-(iv);(b)-(iii);(c)-(i);(d)-(ii) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Q.63➡ | NET December 2018 Consider the vocabulary with only four propositions A,B,C and D. How many models are there for the following sentence? ( ⌐ A ∨ ⌐ B ∨ ⌐ C ∨ ⌐ D) |
| i➥ 8 |
| ii ➥ 7 |
| iii ➥ 15 |
| iv ➥ 16 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.64➡ | NET December 2018 The number of substrings that can be formed from string given by “a d e f b g h n m p” is |
| i➥ 10 |
| ii ➥ 45 |
| iii ➥ 56 |
| iv ➥ 55 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.65➡ | NET December 2018 Consider the following statements related to AND-OR Search algorithm. S 1 : A solution is a subtree that has a goal node at every leaf. S 2 : OR nodes are analogous to the branching in a deterministic environment S 3 : AND nodes are analogous to the branching in a non-deterministic environment. Which one of the following is true referencing the above statements? Choose the correct answer from the code given below: |
| i➥ S1- False, S2- True, S3- True |
| ii ➥ S1- True, S2- True, S3- True |
| iii ➥ S1- False, S2- True, S3- False |
| iv ➥ S1- True, S2- True, S3- False |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.66➡ | NET December 2018 The K-coloring of an undirected graph G=(V,E) is a function C: V➝{0,1,……,K-1} such that c(u)≠c(v) for every edge (u,v) ∈ E Which of the following is not correct? |
| i➥ G has no cycles of odd length |
| ii ➥ G has cycle of odd length |
| iii ➥ G is 2-colorable |
| iv ➥ G is bipartite |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.67➡ | NET December 2018 If a graph (G) has no loops or parallel edges and if the number of vertices(n) in the graph is n≥3, then the graph G is Hamiltonian if (i) deg(v) ≥n/3 for each vertex v (ii) deg(v) + deg(w) ≥ n whenever v and w are not connected by an edge. (iii) E (G) ≥ 1/3 (n − 1 )(n − 2 ) + 2 |
| i➥ (i) and (iii) only |
| ii ➥ (ii) and (iii) only |
| iii ➥ (iii) only |
| iv ➥ (ii) only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.68➡ | NET December 2018 A survey has been conducted on methods of commuter travel. Each respondent was asked to check Bus, Train or Automobile as a major methods of travelling to work. More than one answer was permitted. The results reported were as follows : Bus 30 people; Train 35 people; Automobile 100 people; Bus and Train 15 people; Bus and Automobile 15 people; Train and Automobile 20 people; and all the three methods 5 people. How many people complete the survey form ? |
| i➥ 160 |
| ii ➥ 120 |
| iii ➥ 165 |
| iv ➥ 115 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.69➡ | NET December 2018 A full joint distribution for the Toothache, Cavity and Catch is given in the table below: 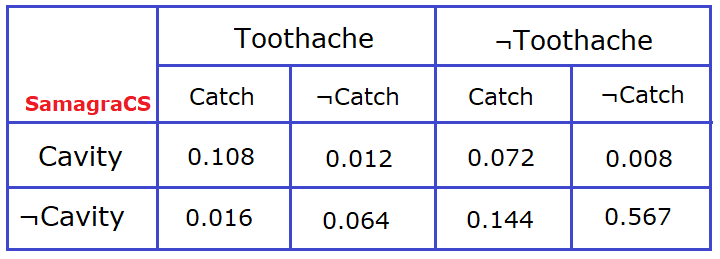 Which is the probability of Cavity, given evidence of Toothache ? |
| i➥ < 0.2, 0.8 > |
| ii ➥ < 0.6, 0.8 > |
| iii ➥ < 0.4, 0.8 > |
| iv ➥ < 0.6, 0.4 > |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.70➡ | NET December 2018 In mathematical logic, which of the following are statements ? (i) There will be snow in January (ii) What is the time now ? (iii) Today is Sunday (iv) You must study Discrete Mathematics. |
| i➥ (iii) and (iv) |
| ii ➥ (i) and (ii) |
| iii ➥ (i) and (iii) |
| iv ➥ (ii) and (iv) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.71➡ | NET December 2018 Consider the statements below : “ There is a country that borders both India and Nepal. “ Which of the following represents the above sentence correctly ? |
| i➥ ∃c Border(Country(c), India ∧ Nepal) |
| ii ➥ ∃c Country(c) ∧ Border(c, India) ∧ Border(c, Nepal) |
| iii ➥ [∃c Country(c)] ⇒ [Border(c,India) ∧ Border(c, Nepal)] |
| iv ➥ ∃c Country(c) ⇒ [ Border(c, India) ∧ Border(c, Nepal)] |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.72➡ | NET December 2018 A box contains six red balls and four green balls. Four balls are selected at random from the box. What is the probability that two of the selected balls will be red and two will be green? |
| i➥ 1/35 |
| ii ➥ 1/14 |
| iii ➥ 1/9 |
| iv ➥ 3/7 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.73➡ | NET June 2018 In a multi-user operating system, 30 requests are made to use a particular resource per hour, on an average. The probability that no requests are made in 40 minutes, when arrival pattern is a poisson distribution, is |
| i➥ e -15 |
| ii ➥ 1-e -15 |
| iii ➥ 1-e -20 |
| iv ➥ e -20 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.74➡ | NET June 2018 Consider the following English sentence : “Agra and Gwalior are both in India”. A student has written a logical sentence for the above English sentence in First-Order Logic using predicate In(x, y), which means x is in y, as follows : In(Agra, India) ⋁ In(Gwalior, India) Which one of the following is correct with respect to the above logical sentence ? |
| i➥ It is syntactically valid but does not express the meaning of the English sentence. |
| ii ➥ It is syntactically valid and expresses the meaning of the English sentence also. |
| iii ➥ It is syntactically invalid but expresses the meaning of the English sentence. |
| iv ➥ It is syntactically invalid and does not express the meaning of the English sentence. |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.75➡ | NET June 2018 Consider the set of all possible five-card poker hands dealt fairly from a standard deck of fifty-two cards. How many atomic events are there in the joint probability distribution? |
| i➥ 2,598,960 |
| ii ➥ 3,468,960 |
| iii ➥ 3,958,590 |
| iv ➥ 2,645,590 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.76➡ | NET June 2018 E is the number of edges in the graph and f is maximum flow in the graph. When the capacities are integers, the runtime of Ford-Fulkerson algorithm is bounded by: |
| i➥ O(E∗f) |
| ii ➥ O(E 2 ∗f) |
| iii ➥ O(E∗f 2 ) |
| iv ➥ None of the above |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.77➡ | NET June 2018 Digital data received from a sensor can fill up 0 to 32 buffers. Let the sample space be S={0, 1, 2, ………., 32} where the sample j denote that j of the buffers are full and P (i) = (1/561)(33 − i ) . Let A denote the event that the even number of buffers are full. Then p(A) is: |
| i➥ 0.515 |
| ii ➥ 0.785 |
| iii ➥ 0.758 |
| iv ➥ 0.485 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.78➡ | NET June 2018 The equivalence of ¬∃ x Q(x) is: |
| i➥ ∃x ¬Q(x) |
| ii ➥ ∀x ¬Q(x) |
| iii ➥ ¬∃ x ¬Q(x) |
| iv ➥ ∀x Q(x) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.79➡ | NET June 2018 If A i = {−i, … −2,−1, 0, 1, 2, . . . . . i} then 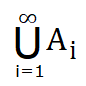 is: is: |
| i➥ Z |
| ii ➥ Q |
| iii ➥ R |
| iv ➥ C |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.80➡ | NET June 2018 If A i = {−i, … −2,−1, 0, 1, 2, . . . . . i} then 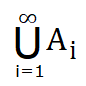 is: is: |
| i➥ Z |
| ii ➥ Q |
| iii ➥ R |
| iv ➥ C |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.81➡ | NET June 2018 Which of the relations on {0, 1, 2, 3} is an equivalence relation? |
| i➥ { (0, 0) (0, 2) (2, 0) (2, 2) (2, 3) (3, 2) (3, 3) } |
| ii ➥ { (0, 0) (1, 1) (2, 2) (3, 3) } |
| iii ➥ { (0, 0) (0, 1) (0, 2) (1, 0) (1, 1) (1, 2) (2, 0) } |
| iv ➥ { (0, 0) (0, 2) (2, 3) (1, 1) (2, 2) } |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.82➡ | NET June 2018 Which of the following is an equivalence relation on the set of all functions from Z to Z? |
| i➥ { (f , g ) | f (x) − g (x) = 1 ∀ x ∈ Z } |
| ii ➥ { (f , g ) | f (0) = g (0) or f (1) = g (1)} |
| iii ➥ { (f , g ) | f (0) = g (1) and f (1) = g (0)} |
| iv ➥ { (f , g ) | f (x) − g (x) = k f or some k ∈ Z } |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.83➡ | NET June 2018 Which of the following statements is true ? |
| i➥ (Z, ≤ ) is not totally ordered |
| ii ➥ The set inclusion relation ⊆ is a partial ordering on the power set of a set S |
| iii ➥ (Z, ≠ ) is a poset |
iv ➥ The directed graph 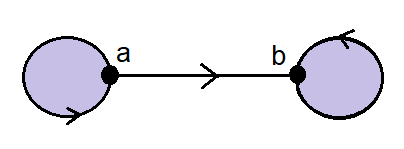 is not a partial order is not a partial order |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.84➡ | NET November 2017 Paper 2 If the time is now 4 O’clock, what will be the time after 101 hours from now? |
| i➥ 9 O’Clock |
| ii ➥ 8 O’Clock |
| iii ➥ 5 O’Clock |
| iv ➥ 4 O’Clock |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.85➡ | NET November 2017 Paper 2 Let A =  and B = and B = Find the boolean product A⊙B of the two matrices. |
i➥ 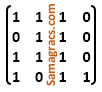 |
ii ➥  |
iii ➥ 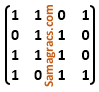 |
iv ➥ 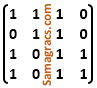 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.86➡ | NET November 2017 Paper 2 How many distinguishable permutations of the letters in the word BANANA are there? |
| i➥ 720 |
| ii ➥ 120 |
| iii ➥ 60 |
| iv ➥ 360 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.87➡ | NET November 2017 Paper 2 Let P and Q be two propositions, ¬ (P ↔ Q) is equivalent to: |
| i➥ P ↔ ¬ Q |
| ii ➥ ¬ P ↔ Q |
| iii ➥ ¬ P ↔ ¬ Q |
| iv ➥ Q → P |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.88➡ | NET November 2017 Paper 2 Negation of the proposition ∃x H(x) is: |
| i➥ ∃x ⌐H(x) |
| ii ➥ ∀x ⌐H(x) |
| iii ➥ ∀x H(x) |
| iv ➥ ⌐x H(x) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.89➡ | NET November 2017 Paper 3 Let P, Q, R and S be Propositions. Assume that the equivalences P ⇔ (Q ∨ ¬ Q) and Q ⇔ R hold. Then the truth value of the formula (P ∧ Q) ⇒ ((P ∧ R) ∨ S) is always: |
| i➥ True |
| ii ➥ False |
| iii ➥ Same as truth table of Q |
| iv ➥ Same as truth table of S |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q.90➡ | NET November 2017 Paper 3 “If X, then Y unless Z” is represented by which of the following formulae in propositional logic? |
| i➥ (X ∧ Y) → ¬ Z |
| ii ➥ (X ∧ ¬ Z) → Y |
| iii ➥ X → (Y ∧ ¬ Z) |
| iv ➥ Y → (X ∧ ¬ Z) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |

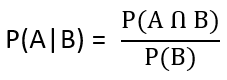
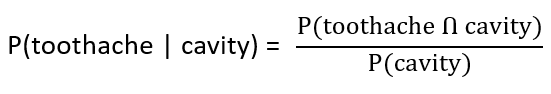

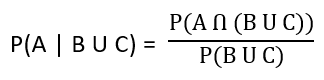
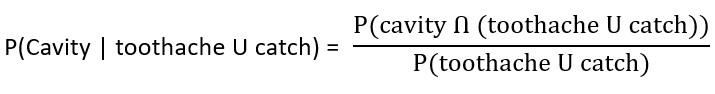
 = 0.4615
= 0.4615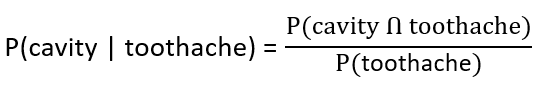
 = 0.6
= 0.6