Boolean Algebra UGC NET
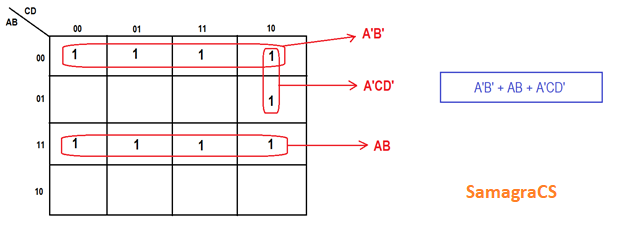
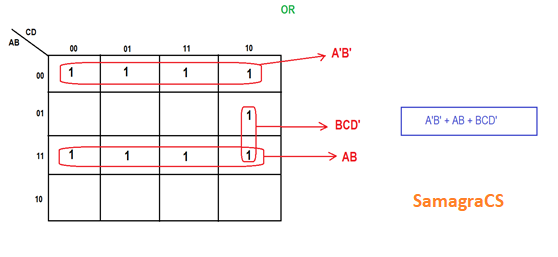
| Question 1➡ | NTA UGC NET November 2020 Simplified expression/s for following Boolean function F(A,B,C,D)=Σ(0,1,2,3,6,12,13,14,15) is/are A) A’B’+AB+A’C’D’ B) A’B’+AB+A’CD’ C) A’B’+AB+BC’D’ D) A’B’+AB+BCD’ Choose the correct answer from the options given below: |
| i ➥ (A) only |
| ii ➥ (B) only |
| iii ➥ (A) and (B) only |
| iv ➥ (B) and (D) only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 2➡ | NTA UGC NET November 2020 What kind of clauses are available in conjunctive normal form? |
| i ➥ Disjunction of literals |
| ii ➥ Disjunction of variables |
| iii ➥ Conjunction of literals |
| iv ➥ Conjunction of variables |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 5➡ | NTA UGC NET December 2019 The Boolean AB+AB’+A’C+AC is unaffected by the value of the Boolean variable ___________. |
| i ➥ A |
| ii ➥ B |
| iii ➥ C |
| iv ➥ A, B & C |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 7➡ | NTA UGC NET June 2019 Which of the following is principal conjunctive normal form for [(pVq) ∧ ~p → ~q] ? |
| i ➥ pV~q |
| ii ➥ pVq |
| iii ➥ ~p Vq |
| iv ➥ ~p V ~q |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 8➡ | NTA UGC NET June 2019 Match List-I with List-II 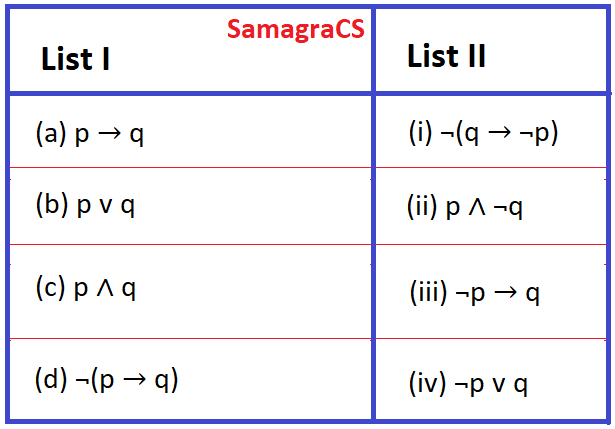 Choose the correct option from those given below: |
| i ➥ (a)-(ii);(b)-(iii);(c)-(i);(d)-(iv) |
| ii ➥ (a)-(ii);(b)-(i);(c)-(iii);(d)-(iv) |
| iii ➥ (a)-(iv);(b)-(i);(c)-(iii);(d)-(ii) |
| iv ➥ (a)-(iv);(b)-(iii);(c)-(i);(d)-(ii) |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 9➡ | NTA UGC NET June 2019 How many different Boolean functions of degree n are there? |
| i ➥ |
| ii ➥ (22)2 |
| iii ➥ 22n-1 |
| iv ➥ |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 17➡ | NTA UGC NET December 2018 The boolean expression A’⋅B+A.B’+A.B is equivalent to |
| i ➥ A+B |
| ii ➥ A.B |
| iii ➥ (A+B)’ |
| iv ➥ A’.B |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 18➡ | NTA UGC NET December 2018 The relation ≤ and < on a boolean algebra are defined as : x ≤ y and only if x ∨ y = y x < y means x ≤ y but x ≠ y x ≥ y means y ≤ x and x > y means y <x Consider the above definitions, which of the following is not true in the boolean algebra ? (i)If x ≤ y and y ≤ z, then x ≤ z (ii)If x ≤ y and y ≤ x, then x=y (iii)If x < y and y < z, then x ≤ y (iv)If x < y and y < z, then x < y |
| i ➥ (iv) only |
| ii ➥ (iii) only |
| iii ➥ (i) and (ii) only |
| iv ➥ (ii) and (iii) only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 19➡ | NTA UGC NET December 2018 Consider the following boolean equations : (i) wx + w(x + y) + x(x + y)=x+wy (ii) (wx’(y+xz’)+w’x’)y=x’y What can you say about the above equations ? |
| i ➥ Both (i) and (ii) are true |
| ii ➥ (i) is true and (ii) is false |
| iii ➥ Both (i) and (ii) are false |
| iv ➥ (i) is false and (ii) is true |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 20➡ | NTA UGC NET December 2018 Find the boolean expression for the logic circuit shown below : (1-NAND gate, 2-NOR gate, 3-NOR gate) 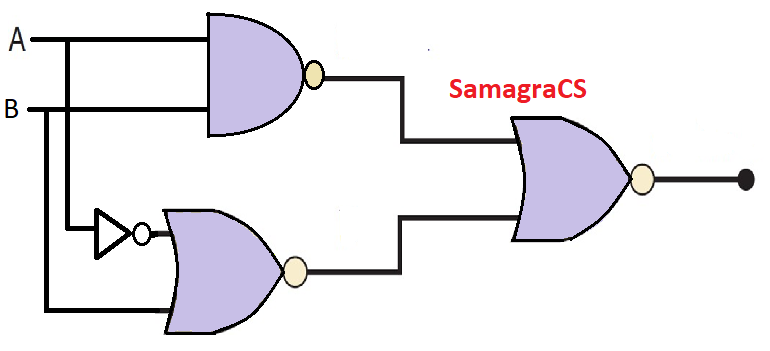 |
| i ➥ AB |
| ii ➥ AB’ |
| iii ➥ A’B’ |
| iv ➥ A’B |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 22➡ | NTA UGC NET December 2018 Which of the following statements are true ? (i) Every logic network is equivalent to one using just NAND gates or just NOR gates. (ii) Boolean expressions and logic networks correspond to labelled acyclic digraphs. (iii) No two Boolean algebras with n atoms are isomorphic. (iv) Non-zero elements of finite Boolean algebras are not uniquely expressible as joins of atoms. |
| i ➥ (i) and (iv) only |
| ii ➥ (i) and (ii) only |
| iii ➥ (i), (ii) and (iii) only |
| iv ➥ (ii), (iii) and (iv) only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 29➡ | NTA UGC NET June 2018 Simplify the following using K-map : F (A, B, C, D) = Σ (0, 1, 2, 8, 9, 12, 13) + d(A, B, C, D) = Σ (10, 11, 14, 15) d stands for don’t care condition. |
| i ➥ A+B’D’ + BC |
| ii ➥ A+B’D’ + B’C’ |
| iii ➥ A’+B’C’ |
| iv ➥ A’+B’C’+B’D’ |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 30➡ | NTA UGC NET November 2017 Paper III Let P, Q, R and S be Propositions. Assume that the equivalences P ⇔ (Q ∨ ¬ Q) and Q ⇔ R hold.Then the truth value of the formula (P ∧ Q) ⇒ ((P ∧ R) ∨ S) is always: |
| i ➥ True |
| ii ➥ False |
| iii ➥ Same as truth table of Q |
| iv ➥ Same as truth table of S |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 34➡ | NTA UGC NET November 2017 Paper II Let A =  and B = and B = Find the boolean product A⊙B of the two matrices. |
i ➥ 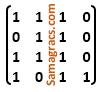 |
ii ➥  |
iii ➥ 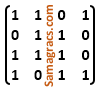 |
iv ➥ 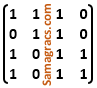 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 35➡ | NTA UGC NET November 2017 Paper II The Boolean function with the Karnaugh map 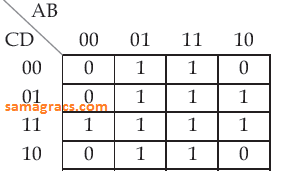 |
| i ➥ (A+C).D+B |
| ii ➥ (A+B).C+D |
| iii ➥ (A+D).C+B |
| iv ➥ (A+C).B+D |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 37➡ | NTA UGC NET November 2017 Paper II Let P and Q be two propositions, ¬ (P ↔ Q) is equivalent to: |
| i ➥ P ↔ ¬ Q |
| ii ➥ ¬ P ↔ Q |
| iii ➥ ¬ P ↔ ¬ Q |
| iv ➥ Q → P |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 38➡ | NTA UGC NET November 2017 Paper II The output of the following combinational circuit is F: 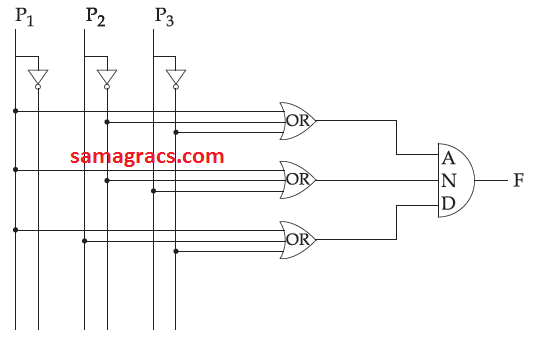 The value of F is : |
| i ➥ P1+P’2P3 |
| ii ➥ P1+P’2P’3 |
| iii ➥ P1 +P2 P’3 |
| iv ➥ P’1 +P2 P3 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |
| Question 38➡ | NTA UGC NET November 2017 Paper II The output of the following combinational circuit is F:  The value of F is : |
| i ➥ P1+P’2P3 |
| ii ➥ P1+P’2P’3 |
| iii ➥ P1 +P2 P’3 |
| iv ➥ P’1 +P2 P3 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Boolean Algebra | Help-Line |