Sparse Matrix in Data Structure
| Contents on Sparse Matrix in Data Structure |
| 1. Introduction to Sparse Matrix 2. Types of Sparse Matrix 3. Implementation of Sparse Matrix 4. Application of Sparse Matrix |
1. Introduction to Sparse Matrix : As we know the two dimension array is a matrix which is a combinations of row and column in mathematical application. Two dimension array matrix contain maximum zero entries is called sparse matrices. If the given matrix most of the elements are non-zero then the given matrix considered dense. Sparse Matrices having relatively high proportion of zero entries. there are two general type of n-square sparse matrices. 1. Triangular matrix. 2. Tridiagonal matrix.  |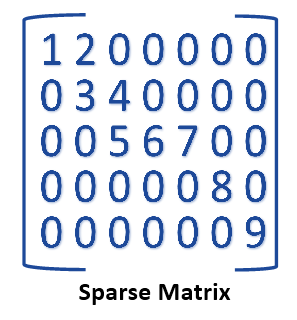
| 2. Types of Sparse Matrix : There are two general type of n-square sparse matrices.  1. Triangular matrix. 2. Tridiagonal matrix.2.1 Triangular matrix. In triangular Matrix where all entries above the main diagonal are zero or equivalently. Where nonzero entries can only occur main diagonal or below the main diagonal.  |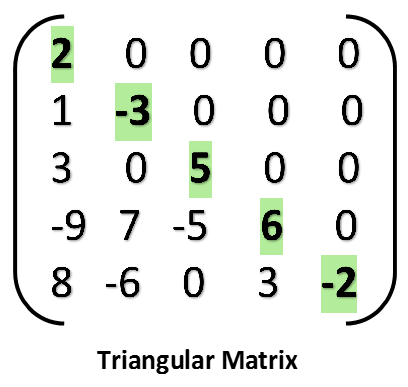
| 2.2. Tridiagonal matrix. In triangular Matrix where nonzero entries can only occur on the main diagonal or on elements immediately above the main diagonal or below the main diagonal.  |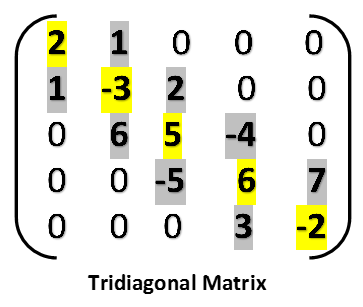
| 3. Implementation of Sparse Matrix Sparse can be implemented using array and Linked list. Using ArrayTwo Dimension array is used to represent a sparse matrix. There are three rows to represent it Row,Column and Value. Using linked list sparse matrix implemented with four field Row,Column, value and Next_node. |
| 4. Application of Sparse Matrix combinatorics. network theory. numerical analysis. |