DFA|Deterministic Finite Automata Questions-Answers
| Q1➡ |DFA According to the 5-tuple representation i.e. FA= {Q, ∑, δ, q, F} Statement 1: q ϵ Q’; Statement 2: FϵQ |
| i ➥ Statement 1 is false, Statement 2 is true |
| ii ➥ Statement 1 may be true, Statement 2 is false |
| iii ➥ Statement 1 is false, Statement 2 may be true |
| iv ➥ Statement 1 is true, Statement 2 is false |
Show Answer With Best Explanation
| Q2➡ |DFA δˆ tells us the best: |
| i ➥ the final state has been reached |
| ii ➥ Kleene operation is performed on the set |
| iii ➥ how the DFA S behaves on a word u |
| iv ➥ the state is the dumping state |
Show Answer With Best Explanation
| Q3➡ |DFA For a DFA accepting binary numbers whose decimal equivalent is divisible by 4, what are all the possible remainders? |
| i ➥ 0 |
| ii ➥ 0,2,4 |
| iii ➥ 0,1,2,3 |
| iv ➥ 0,2 |
Show Answer With Best Explanation
| Q4➡ |DFA Which of the following option is correct? A= {{abc, aaba}. {ε, a, bb}} |
| i ➥ ε₵A |
| ii ➥ abca ₵ A |
| iii ➥ ε may not belong to A |
| iv ➥ abcbb ₵ A |
Show Answer With Best Explanation
| Q5➡ |DFA Given: L1= {xϵ ∑|x contains even no’s of 0’s} L2= {xϵ ∑|x contains odd no’s of 1’s} No of final states in Language L1 U L2? |
| i ➥ 4 |
| ii ➥ 3 |
| iii ➥ 2 |
| iv ➥ 1 |
Show Answer With Best Explanation
| Q6➡ |DFA The maximum number of transition which can be performed over a state in a DFA? ∑= {a, b, c} |
| i ➥ 4 |
| ii ➥ 3 |
| iii ➥ 2 |
| iv ➥ 1 |
Show Answer With Best Explanation
| Q7➡ |DFA How many languages are over the alphabet R? |
| i ➥ uncountable infinite |
| ii ➥ countably finite |
| iii ➥ uncountable finite |
| iv ➥ countably infinite |
Show Answer With Best Explanation
| Q8➡ |DFA The maximum sum of in degree and out degree over a state in a DFA can be determined as: ∑= {a, b, c, d} |
| i ➥ 4+0 |
| ii ➥ 4+16 |
| iii ➥ 4+4 |
| iv ➥ depends on the Language |
Show Answer With Best Explanation
| Q10➡ |DFA The sum of minimum and maximum number of final states for a DFA n states is equal to: |
| i ➥ n-1 |
| ii ➥ n+2 |
| iii ➥ n+1 |
| iv ➥ n |
Show Answer With Best Explanation
| Q11➡ |DFA The number of states in a minimal deterministic finite automaton corresponding to the language L = { an | n≥4 } is |
DFA|Deterministic Finite Automata Questions-Answers
| i ➥ 6 |
| ii ➥ 5 |
| iii ➥ 4 |
| iv ➥ 3 |
Show Answer With Best Explanation
| Q12➡ |DFA State whether TRUE or FALSE (i) In NDFA, the transition function δ: Q × Σ → 2Q (ii) NDFA does not permit empty string transitions |
| i ➥ (i) True (ii) True |
| ii ➥ (i) False (ii) True |
| iii ➥ (i) True (ii) False |
| iv ➥ (i) False (ii) False |
Show Answer With Best Explanation
| Q13➡ |DFA two DFA’s M1 and M2. They are equivalent if: |
| i ➥ M1 and M2 has the same number of final states |
| ii ➥ M1 and M2 accepts the same language i.e L(M1)=L(M2) |
| iii ➥ M1 and M2 has the same number of states |
| iv ➥ None |
Show Answer With Best Explanation
| Q14➡ |DFA Can a DFA simulate NFA? |
| i ➥ Yes |
| ii ➥ No |
| iii ➥ Depends on NFA |
| iv ➥ Sometimes |
Show Answer With Best Explanation
| Q15➡ |DFA What are the final states of the DFA generated from the following NFA? 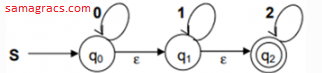 |
| i ➥ q0, [q1, q2] |
| ii ➥ [q0, q1], q2 |
| iii ➥ q0, q1, q2 |
| iv ➥ [q0, q1], [q0, q2], [ ] |
Show Answer With Best Explanation
| Q16➡ |DFA Consider the regular grammar: S → Xa | Ya X → Za Z → Sa | ϵ Y → Wa W → Sa where S is the starting symbol, the set of terminals is {a} and the set of non-terminals is {S, W, X, Y, Z}. We wish to construct a deterministic finite automaton (DFA) to recognize the same language. What is the minimum number of states required for the DFA? |
| i ➥ 5 |
| ii ➥ 4 |
| iii ➥ 3 |
| iv ➥ 2 |
Show Answer With Best Explanation
| Q17➡ |DFA The number of states in the minimal deterministic finite automaton corresponding to the regular expression (0 + 1) * (10) is __. |
| i ➥ 6 |
| ii ➥ 5 |
| iii ➥ 4 |
| iv ➥ 3 |
Show Answer With Best Explanation
Q18➡ |DFA 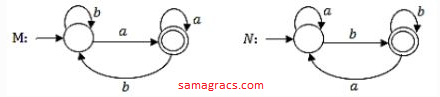 Consider the DFAs M and N given above. The number of states in a minimal DFA that accepts the language L(M) ∩ L(N) is __. |
| i ➥ 4 |
| ii ➥ 3 |
| iii ➥ 1 |
| iv ➥ 2 |
Show Answer With Best Explanation
DFA|Deterministic Finite Automata Questions-Answers
| Q19➡ |DFA The number of states in the minimum sized DFA that accepts the language defined by the regular expression (0+1)(0+1)(0+1) is_________. |
| i ➥ 3 |
| ii ➥ 5 |
| iii ➥ 2 |
| iv ➥ 9 |
Show Answer With Best Explanation
| Q20➡ |DFA The minimum possible number of a deterministic finite automation that accepts the regular language L = {w1aw2 | w1, w2 ∈ {a,b}*, |w1| = 2,|w2| ≥ 3} is______. |
| i ➥ 10 |
| ii ➥ 8 |
| iii ➥ 12 |
| iv ➥ 11 |
Show Answer With Best Explanation
| Q21➡ |DFA A binary string is divisible by 4 if and only if it ends with: |
| i ➥ 1100 |
| ii ➥ 0011 |
| iii ➥ 100 |
| iv ➥ 1000 |
Show Answer With Best Explanation
| Q22➡ |DFA Given Language: {x | it is divisible by 3} The total number of final states to be assumed in order to pass the number constituting {0, 1} is |
| i ➥ 1 |
| ii ➥ 0 |
| iii ➥ 3 |
| iv ➥ 2 |
Show Answer With Best Explanation
| Q2➡ |DFA |
| i ➥ |
| ii ➥ |
| iii ➥ |
| iv ➥ |
Show Answer With Best Explanation
| You should also practice on below topics Regular Language Mode Deterministic Finite Automaton (DFA), Non-Deterministic Finite Automaton (NDFA), Equivalence of DFA and NDFA, Regular Languages, Regular Grammars, Regular Expressions, |
