NFA | Non Deterministic Finite Automata Questions-Answers – Theory of Computation
| Q1➡ | NET June 2021 Which of the following languages are not regular? A. L={ (01)n0k | n > k, k>=0 } B. L={ cnbkan+k | n >= 0, k>=0 } C. L={ 0n1k | n≠k } Choose the correct answer from the options given below: |
| i ➥ A and C only |
| ii ➥ A and B only |
| iii ➥ A, B and C |
| iv ➥ B and C only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q2➡ | NET June 2021 What language is accepted by the pushdown automaton M=({q0, q1, q2}, {a, b}, {a, b, z}, δ, q0, z, {q2}) with δ(q0, a, a) ={ (q0, aa) }; δ(q0, b, a) ={(q0, ba)} δ(q0, a, b) ={ (q0, ab) }; δ(q0, b, b) ={ (q0, bb) } δ(q0, a, z) ={ (q0, az) }; δ(q0, b, z) ={ (q0, bz) } δ(q0, λ, b) ={ (q1, b) }; δ(q0, λ, a) ={ (q1, a) } δ(q1, a, a) ={ (q1, λ) }; δ(q1, b, b) ={ (q1, λ) } δ(q1, λ, z) ={ (q2, z) }? |
| i ➥ L = { w | na(w) <= nb(w), w Є {a, b}+}} |
| ii ➥ L = { w | na(w) = nb(w), w Є {a, b}+}} |
| iii ➥ L = { w | nb(w) <= na(w), w Є {a, b}+}} |
| iv ➥ L= {wwR | w Є {a, b}+} |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q3➡ | NET June 2021 L1 = { 0n1n0m | n>=1, m>=1 } L2 = { 0n1m0m | n>=1, m>=1 } L3 = { 0n1n0n | n>=1} Which of the following are correct statements? A. L3 =L1 ∩ L2 B. L1 and L2 are context free languages but L3 is not a context free language C. L1 and L2 are not context free languages but L3 is a context free language D. L1 is a subset of L3 Choose the correct answer from the options given below: |
| i ➥ A and C only |
| ii ➥ A and D only |
| iii ➥ A only |
| iv ➥ A and B only |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q4➡ | NET June 2021 Any string of terminals that can generated by the following context free grammar (where S is start non-terminal symbol) S→XY X→0X|1X|0 Y→Y0|Y1|0 |
| i ➥ has at least one 1 |
| ii ➥ has no consecutive 0’s or 1’s |
| iii ➥ should end with 0 |
| iv ➥ has at least two 0’s |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q5➡ | NET June 2021 Match List I with List II 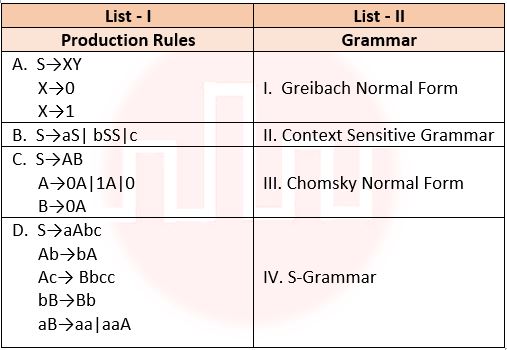 Choose the correct answer from the options below: |
| i ➥ A – III, B -I , C – IV, D – II |
| ii ➥ A – III, B -II , C – I, D – IV |
| iii ➥ A – III, B -IV, C – I, D – II |
| iv ➥ A – IV, B -III , C – I, D – II |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q6➡ | NET June 2021 What is the minimum number of states required to the finite automaton equivalent to the transition diagram given below?  |
| i ➥ 3 |
| ii ➥ 4 |
| iii ➥ 5 |
| iv ➥ 6 |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q7➡ | NET June 2021 Given below are two statements Statement I: The family of context free languages is closed under homomorphism Statement II: The family of context free languages is closed under reversal. In light of the above statements, choose the correct answer from the options given below |
| i ➥ Both Statement I and Statement II are false |
| ii ➥ Both Statement I and Statement II are true |
| iii ➥ Statement I is false but Statement II is true |
| iv ➥ Statement I is true but Statement II is false |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q8➡ | NET June 2021 Find the regular expression for the language accepted by the automata given below. 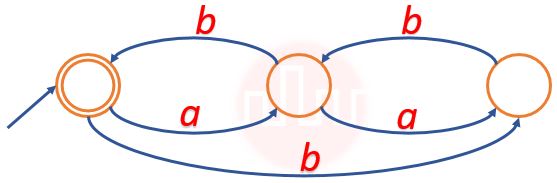 |
| i ➥ (a+b)ab(ab+bb+ aa*(a+b)ab)* |
| ii ➥ (aa*(a+b)ab)* |
| iii ➥ a*(a+b)ab(ab+bb+ aa*(a+b)ab)* |
| iv ➥ a*ab(ab+bb+ aa*(a+b)ab)* |
Show Answer With Best Explanation
| More Discussion | Explanation On YouTube | Learn Topic Wise | Help-Line |
| Q➡ |NFA Which of the following options is correct? Statement 1: Initial State of NFA is Initial State of DFA. Statement 2: The final state of DFA will be every combination of final state of NFA. |
| i ➥ Statement 1 can be true and Statement 2 is true |
| ii ➥ Statement 1 is false and Statement 2 is also false |
| iii ➥ Statement 1 is true and Statement 2 is true |
| iv ➥ Statement 1 is true and Statement 2 is false |
Show Answer With Best Explanation
| Q➡ |NFA Given Language: L= {ab U aba}* If X is the minimum number of states for a DFA and Y is the number of states to construct the NFA, |X-Y|=? |
| i ➥ 4 |
| ii ➥ 3 |
| iii ➥ 2 |
| iv ➥ 1 |
Show Answer With Best Explanation
| Q➡ |NFA An automaton that presents output based on previous state or current input: |
| i ➥ Transducer |
| ii ➥ Acceptor |
| iii ➥ Classifier |
| iv ➥ None of the mentioned. |
Show Answer With Best Explanation
| Q➡ |NFA If NFA of 6 states excluding the initial state is converted into DFA, maximum possible number of states for the DFA is ? |
| i ➥ 128 |
| ii ➥ 127 |
| iii ➥ 64 |
| iv ➥ 32 |
Show Answer With Best Explanation
| Q➡ |NFA NFA, in its name has ’non-deterministic’ because of : |
| i ➥ The choice of path is non-deterministic |
| ii ➥ The state to be transited next is non-deterministic |
| iii ➥ The result is undetermined |
| iv ➥ All of the Above |
Show Answer With Best Explanation
| Q➡ |NFA Which of the following is correct proposition? Statement 1: Non determinism is a generalization of Determinism. Statement 2: Every DFA is automatically an NFA |
| i ➥ Statement 2 is false and Statement 1 is false |
| ii ➥ Statement 1 is false because Statement 2 is false |
| iii ➥ Statement 2 is correct because Statement 2 is correct |
| iv ➥ Statement 1 is correct because Statement 2 is correct |
Show Answer With Best Explanation
| Q➡ |NFA Given Language L= {xϵ {a, b}*|x contains aba as its substring} Find the difference of transitions made in constructing a DFA and an equivalent NFA? |
| i ➥ 4 |
| ii ➥ 3 |
| iii ➥ 2 |
| iv ➥ Cannot be able to determined. |
Show Answer With Best Explanation
| Q➡ |NFA The construction time for DFA from an equivalent NFA (m number of node)is: |
| i ➥ O(2m) |
| ii ➥ O(logm) |
| iii ➥ O(m2) |
| iv ➥ O(m) |
Show Answer With Best Explanation
| Q➡ |NFA If n is the length of Input string and m is the number of nodes, the running time of DFA is x that of NFA.Find x? |
| i ➥ log m |
| ii ➥ 1/m |
| iii ➥ 2m |
| iv ➥ 1/m2 |
Show Answer With Best Explanation
| Q➡ |NFA Which of the following option is correct? |
| i ➥ NFA is slower to process and its representation uses less memory than DFA |
| ii ➥ DFA is slower to process and its representation uses less memory than NFA |
| iii ➥ NFA is slower to process and its representation uses more memory than DFA |
| iv ➥ DFA is faster to process and its representation uses less memory than NFA |
Show Answer With Best Explanation
| Q➡ |NFA Subset Construction method refers to: |
| i ➥ Eliminating Null references |
| ii ➥ ε-NFA to NFA |
| iii ➥ Conversion of NFA to DFA |
| iv ➥ DFA minimization |
Show Answer With Best Explanation
| Q➡ |NFA Given Language: Ln= {xϵ {0,1} * | |x|≥n, nth symbol from the right in x is 1} How many state are required to execute L3 using NFA? |
| i ➥ 5 |
| ii ➥ 14 |
| iii ➥ 15 |
| iv ➥ 16 |
Show Answer With Best Explanation
| Q➡ |NFA Which of the following does the given NFA represent? 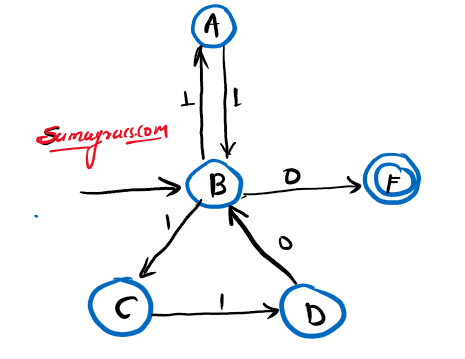 |
| i ➥ {11, 110} * {0} |
| ii ➥ {00, 110} * {1} |
| iii ➥ {11, 101} * {01} |
| iv ➥ {110, 01} * {11} |
Show Answer With Best Explanation
| Q➡ |NFA The number of transitions required to convert the following into equivalents DFA: 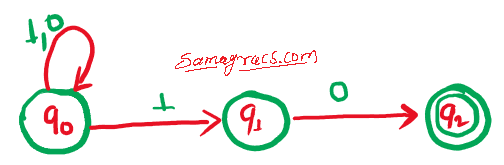 |
| i ➥ 3 |
| ii ➥ 2 |
| iii ➥ 1 |
| iv ➥ 0 |
Show Answer With Best Explanation
| Q➡ |NFA If L is a regular language, Lc and Lr both will be: |
| i ➥ Cannot be said |
| ii ➥ One of them will be accepted |
| iii ➥ Accepted by NFA |
| iv ➥ Rejected by NFA |
Show Answer With Best Explanation
| Q➡ |NFA In NFA, this very state is like dead-end non final state: |
| i ➥ REJECT |
| ii ➥ START |
| iii ➥ ACCEPT |
| iv ➥ DISTINCT |
Show Answer With Best Explanation
| Q➡ |NFA The production of form non-terminal -> ε is called: |
| i ➥ Epsilon Production |
| ii ➥ Sigma Production |
| iii ➥ Null Production |
| iv ➥ All of the Above |
Show Answer With Best Explanation
| Q➡ |NFA Which of the following is a regular language? |
| i ➥ String with even number of Zero’s |
| ii ➥ Palindrome string |
| iii ➥ String whose length is a sequence of prime numbers |
| iv ➥ Which of the following is a regular language? |
Show Answer With Best Explanation
| Q➡ |NFA Which of the following recognizes the same formal language as of DFA and NFA? |
| i ➥ Robin-Scott Construction |
| ii ➥ Power set Construction |
| iii ➥ Subset Construction |
| iv ➥ All of the Above |
Show Answer With Best Explanation
| Q➡ |NFA Regarding the power of recognition of languages, which of the following statements is false? |
| i ➥ Non-deterministic Turing machines are equivalent to deterministic Push-down automata. |
| ii ➥ Non-deterministic Push-down automata are equivalent to deterministic Push- down automata. |
| iii ➥ The non-deterministic finite-state automata are equivalent to deterministic finite-state automata. |
| iv ➥ Both A and B |
Show Answer With Best Explanation
| Q➡ |NFA Let Nf and Np denote the classes of languages accepted by non-deterministic finite automata and non-deterministic push-down automata, respectively. Let Df and Dp denote the classes of languages accepted by deterministic finite automata and deterministic push-down automata, respectively. Which one of the following is TRUE? |
| i ➥ Df = Nf and Dp ⊂ Np |
| ii ➥ Df = Nf and Dp = Np |
| iii ➥ Df ⊂ Nf and Dp = Np |
| iv ➥ Df ⊂ Nf and Dp ⊂ Np |
Show Answer With Best Explanation
| Q➡ |NFA Which one of the following is FALSE? |
| i ➥ Complement of every context-free language is recursive. |
| ii ➥ Every non-deterministic PDA can be converted to an equivalent deterministic PDA. |
| iii ➥ There is unique minimal DFA for every regular language. |
| iv ➥ Every NFA can be converted to an equivalent PDA. |
Show Answer With Best Explanation
| Q➡ |NFA Which of the following pairs have DIFFERENT expressive power? |
| i ➥ Deterministic push down automata (DPDA) and Non-deterministic push down automata (NFDA) |
| ii ➥ Single-tape Turning machine and multi-tape Turning machine |
| iii ➥ Deterministic finite automata (DFA) and Non-deterministic finite automata (NFA) |
| iv ➥ Deterministic single-tape Turning machine and Non-deterministic single tape Turning machine |
Show Answer With Best Explanation
Q➡ |NFA 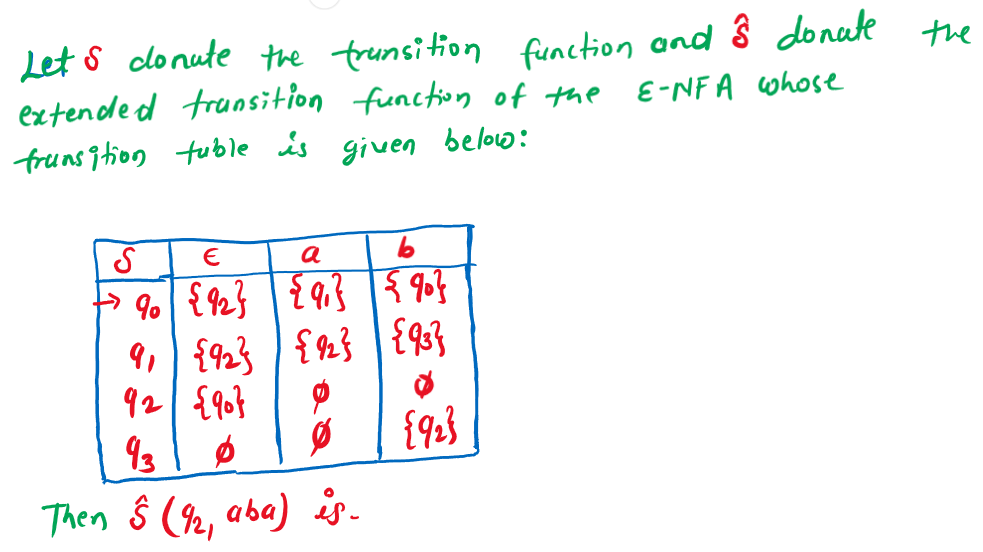 |
| i ➥ {q0,q1,q2} |
| ii ➥ {q0,q1,q3} |
| iii ➥ {q0,q2,q3} |
| iv ➥ ∅ |
Show Answer With Best Explanation
| You should also practice on below topics Regular Language Mode Deterministic Finite Automaton (DFA), Non-Deterministic Finite Automaton (NDFA), Equivalence of DFA and NDFA, Regular Languages, Regular Grammars, Regular Expressions, |

 =1, m>=1 }”>
=1, m>=1 }”>