Regular Languages Questions-Answers- Theory of Computation
| Q1➡ |Regular Languages A regular language over an alphabet a is one that can be obtained from |
| i ➥ kleene |
| ii ➥ concatenation |
| iii ➥ union |
| iv ➥ All of the mentioned |
Show Answer With Best Explanation
| Q2➡ |Regular Languages Regular expression {0,1} is equivalent to |
| i ➥ 0 / 1 |
| ii ➥ 0 + 1 |
| iii ➥ 0 U 1 |
| iv ➥ All of the mentioned |
Show Answer With Best Explanation
| Q3➡ |Regular Languages Precedence of regular expression in decreasing order is |
| i ➥ + , a , * |
| ii ➥ . , + , * |
| iii ➥ . , * , + |
| iv ➥ *, . , + |
Show Answer With Best Explanation
| Q4➡ |Regular Languages Regular expression Φ* is equivalent to |
| i ➥ Φ |
| ii ➥ 0 |
| iii ➥ ϵ |
| iv ➥ 1 |
Show Answer With Best Explanation
| Q5➡ |Regular Languages a? is equivalent to |
| i ➥ a+ϵ |
| ii ➥ a+Φ |
| iii ➥ a |
| iv ➥ wrong expression |
Show Answer With Best Explanation
| Q6➡ |Regular Languages ϵL is equivalent to |
| i ➥ Lϵ |
| ii ➥ L |
| iii ➥ Φ |
| iv ➥ both i and ii |
Show Answer With Best Explanation
| Q7➡ |Regular Languages (a+b)* is equivalent to |
| i ➥ (b*a*)* |
| ii ➥ b*a* |
| iii ➥ a*b* |
| iv ➥ none of the above |
Show Answer With Best Explanation
| Q8➡ |Regular Languages Which of the following pair of regular expression are not equivalent? |
| i ➥ (ab)* and a*b* |
| ii ➥ x+ and x*x+ |
| iii ➥ x(xx)* and (xx)*x |
| iv ➥ 1(01)* and (10)*1 |
Show Answer With Best Explanation
| Q9➡ |Regular Languages Consider following regular expression i)(a/b)* ii) (a*/b*)* iii) ((ϵ/a)b*)* Which of the following statements is correct |
| i ➥ i,ii are equal and i,iii are not |
| ii ➥ ii,iii are equal and i,ii are not |
| iii ➥ i,ii are equal and ii,iii are not |
| iv ➥ all are equal |
Show Answer With Best Explanation
| Q10➡ |Regular Languages There are __ tuples in finite state machine. |
| i ➥ 6 |
| ii ➥ 4 |
| iii ➥ 5 |
| iv ➥ unlimited |
Show Answer With Best Explanation
| Q11➡ |Regular Languages Transition function maps. |
| i ➥ Q * Σ -> Q |
| ii ➥ Σ * Σ -> Q |
| iii ➥ Q * Q -> Σ |
| iv ➥ Σ * Q -> Σ |
Show Answer With Best Explanation
| Q12➡ |Regular Languages Number of states require to accept string ends with 10. |
| i ➥ 1 |
| ii ➥ 2 |
| iii ➥ 3 |
| iv ➥ 4 |
Show Answer With Best Explanation
| Q13➡ |Regular Languages Extended transition function is . |
| i ➥ Q* * Σ* -> Σ |
| ii ➥ Q * Σ -> Σ |
| iii ➥ Q * Σ -> Q |
| iv ➥ Q * Σ* -> Q |
Show Answer With Best Explanation
| Q14➡ |Regular Languages .δ*(q,ya) is equivalent to . |
| i ➥ δ(δ*(q,y),a) |
| ii ➥ δ(q,ya) |
| iii ➥ independent from δ notation |
| iv ➥ δ((q,y),a) |
Show Answer With Best Explanation
| Q15➡ |Regular Languages String X is accepted by finite automata if . |
| i ➥ δ*(Q0,x) E A |
| ii ➥ δ(q,x) E A |
| iii ➥ δ(Q0,x) E A |
| iv ➥ δ*(q,x) E A |
Show Answer With Best Explanation
| Q16➡ |Regular Languages Languages of a automata is |
| i ➥ If it halts |
| ii ➥ If it is accepted by automata |
| iii ➥ If automata touch final state in its life time |
| iv ➥ All language are language of automata |
Show Answer With Best Explanation
| Q17➡ |Regular Languages Language of finite automata is. |
| i ➥ Type 3 |
| ii ➥ Type 2 |
| iii ➥ Type 1 |
| iv ➥ Type 0 |
Show Answer With Best Explanation
| Q18➡ |Regular Languages Finite automata requires minimum____ number of stacks. |
| i ➥ 1 |
| ii ➥ 2 |
| iii ➥ 0 |
| iv ➥ 3 |
Show Answer With Best Explanation
| Q19➡ |Regular Languages Number of final state require to accept Φ in minimal finite automata. |
| i ➥ 3 |
| ii ➥ 2 |
| iii ➥ 1 |
| iv ➥ No final state requires |
Show Answer With Best Explanation
| Q20➡ |Regular Languages How many DFA’s exits with two states over input alphabet {0,1} ? |
| i ➥ 64 |
| ii ➥ 32 |
| iii ➥ 16 |
| iv ➥ 26 |
Show Answer With Best Explanation
| Q21➡ |Regular Languages The basic limitation of finite automata is that |
| i ➥ It sometimes fails to recognize regular grammar. |
| ii ➥ It can remember arbitrary large amount of information |
| iii ➥ It can’t remember arbitrary large amount of information |
| iv ➥ It sometimes recognize grammar that are not regular |
Show Answer With Best Explanation
| Q22➡ |Regular Languages Regular expression for all strings starts with ab and ends with bba is. |
| i ➥ ab(a+b)*bba |
| ii ➥ ab(ab)*bba |
| iii ➥ ababbba |
| iv ➥ All of the Above |
Show Answer With Best Explanation
| Q23➡ |Regular Languages Number of states require to simulate a computer with memory capable of storing ‘3’ words each of length ‘8’. |
| i ➥ 2(3+8) |
| ii ➥ 2(3*8) |
| iii ➥ 3 * 28 |
| iv ➥ 3 * 38 |
Show Answer With Best Explanation
| Q24➡ |Regular Languages FSM with output capability can be used to add two given integer in binary representation. This is |
| i ➥ true |
| ii ➥ false |
| iii ➥ may be true |
| iv ➥ can’t say anything |
Show Answer With Best Explanation
| Q25➡ |Regular Languages L is a regular Language if and only If the set of__________classes of IL is finite. |
| i ➥ Myhill |
| ii ➥ Nerode |
| iii ➥ Reflexive |
| iv ➥ Equivalence |
Show Answer With Best Explanation
| Q26➡ |Regular Languages Which of the following does not represents the given language? Language: {0,01} |
| i ➥ {0} ^ {01} |
| ii ➥ {0} U {0}{1} |
| iii ➥ {0} U {01} |
| iv ➥ 0+01 |
Show Answer With Best Explanation
| Q27➡ |Regular Languages According to the given language, which among the following expressions does it corresponds to? Language L={xϵ{0,1}|x is of length 4 or less} |
| i ➥ (0+1)4 |
| ii ➥ (01)4 |
| iii ➥ (0+1+ε)4 |
| iv ➥ (0+1+0+1+0+1+0+1)4 |
Show Answer With Best Explanation
| Q28➡ |Regular Languages Which among the following looks similar to the given expression? ((0+1). (0+1)) * |
| i ➥ {xϵ {0,1} |x is all binary number with odd length} |
| ii ➥ {xϵ {0,1} *|x is all binary number with even length} |
| iii ➥ {xϵ {0,1} |x is all binary number with even length} |
| iv ➥ {xϵ {0,1} *|x is all binary number with odd length} |
Show Answer With Best Explanation
| Q29➡ |Regular Languages Concatenation Operation refers to which of the following set operations: |
| i ➥ Dot |
| ii ➥ Kleene |
| iii ➥ Union |
| iv ➥ none |
Show Answer With Best Explanation
| Q30➡ |Regular Languages Concatenation of R with Ф outputs: |
| i ➥ Ф |
| ii ➥ R |
| iii ➥ R.Ф |
| iv ➥ i and ii |
Show Answer With Best Explanation
| Q31➡ |Regular Languages RR* can be expressed in which of the forms: |
| i ➥ R |
| ii ➥ R+ U R- |
| iii ➥ R+ |
| iv ➥ R- |
Show Answer With Best Explanation
| Q32➡ |Regular Languages The Language L = {ap| p is prime } is : |
| i ➥ regular |
| ii ➥ accepted by NFA with ε |
| iii ➥ not regular |
| iv ➥ none of the above |
Show Answer With Best Explanation
| Q33➡ |Regular Languages If L1 and L2 are two regular language defined as L1 = (000, 001, 0, 010) and L2 = ( 00, 01, 0), then the number of strings in L1 ∪ L2 will be |
| i ➥ 8 |
| ii ➥ 7 |
| iii ➥ 6 |
| iv ➥ 5 |
Show Answer With Best Explanation
| Q34➡ |Regular Languages If L1 and L2 are context free language and R is a regular set. Which one of the languages below is not necessarily a context free language? |
| i ➥ L1∪L2 |
| ii ➥ L1∪R |
| iii ➥ L1∩L2 |
| iv ➥ L1L2 |
Show Answer With Best Explanation
| Q35➡ |Regular Languages Which one of the following is TRUE? |
| i ➥ Every regular grammar is not LL(1) and every regular set has an LR(1) grammar |
| ii ➥ Every regular grammar is LL(1) and every regular has an LR(1) grammar |
| iii ➥ Every regular grammar is not LL(1) and every regular set does not have an LR(1) grammar |
| iv ➥ Every regular grammar is LL(1) and every regular set does not have an LR(1) grammar |
Show Answer With Best Explanation
| Q36➡ |Regular Languages Which of the following is true? |
| i ➥ Infinite union of finite set is regular |
| ii ➥ The union of two non regular set is not regular |
| iii ➥ Every finite subset of non-regular set is regular |
| iv ➥ Every subset of a regular set is regular |
Show Answer With Best Explanation
Q37➡ |Regular Languages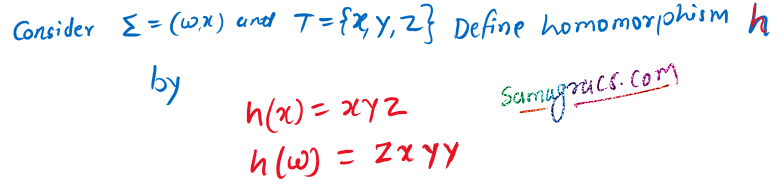 If L is the regular language denoted by T= (w + x*)(ww)*, then the regular language h(L) is given by |
| i ➥ (zxyy + (xzy)* (zxyy zxyy) |
| ii ➥ (zxyy + xyz) (zxyy)* |
| iii ➥ (zxyy + (xzy)*) (zxyy zxyy)* |
| iv ➥ (z x yy + xy) (z x yy) |
Show Answer With Best Explanation
| Q38➡ |Regular Languages Given the following two languages : L1 = {uwwRν | u, v, w ∈ {a, b}+} L2 = {uwwRν | u, ν, w ∈ {a, b}+, |u| > |ν|} Which of the following is correct ? |
| i ➥ L1 is not regular language and L2 is regular language. |
| ii ➥ L1 is regular language and L2 is not regular language. |
| iii ➥ Both L1 and L2 are not regular languages. |
| iv ➥ Both L1 and L2 are regular languages |
Show Answer With Best Explanation
| Q39➡ |Regular Languages The regular grammar for the language L = {anbm | n + m is even} is given by |
| i ➥ S → S1 | S2 S1 → a S1| A1 A1 → b A1| λ S2 → aaS2| A2 A2 → b A2| λ |
| ii ➥ S → S1 | S2 S1 → a S1| aA1 S2 → aaS2 | A2 A1 → b A1| λ A2 → b A2| λ |
| iii ➥ S → S1 | S2 S1 → aaa S1| aA1 S2 → aaS2| A2 A1 → b A1| λ A2 → b A2| λ |
| iv ➥ S → S1 | S2 S1 → aa S1 | A1 S2 → aaS2 | aA2 A1 → bbA1 | λ A2 → bbA | b |
Show Answer With Best Explanation
| Q40➡ |Regular Languages Consider the following two languages : L1 = {0i1j| gcd (i, j) = 1} L2 is any subset of 0*. Which of the following is correct ? |
| i ➥ L1 is not regular and L2* is regular |
| ii ➥ L1 is regular and L2* is not regular |
| iii ➥ Both L1 and L2* are not regular languages |
| iv ➥ Both L1 and L2* are regular languages |
Show Answer With Best Explanation
| Q41➡ |Regular Languages Which of the following are not regular? (1) Strings of even number of a’s. (2) Strings of a’s, whose length is a prime number. (3) Set of all palindromes made up of a’s and b’s. (4) Strings of a’s whose length is a perfect square. |
| i ➥ (1) and (2) only |
| ii ➥ (1), (2) and (3) only |
| iii ➥ (2), (3) and (4) only |
| iv ➥ (2) and (4) only |
Show Answer With Best Explanation
| Q42➡ |Regular Languages Pumping lemma for regular language is generally used for proving: |
| i ➥ a given grammar is not regular |
| ii ➥ a given grammar is regular |
| iii ➥ a given grammar is ambiguous |
| iv ➥ whether two given regular expressions are equivalent |
Show Answer With Best Explanation
| Q43➡ |Regular Languages Which of the following language is regular : |
| i ➥ L = { an bm cn|n, m ≥ 1 } |
| ii ➥ L = { an bm|n, m ≥ 1 } |
| iii ➥ L = { an bm cn dm|n, m ≥ 1 } |
| iv ➥ L = { an bn| n ≥ 1 } |
Show Answer With Best Explanation
| Q44➡ |Regular Languages Consider the set of all words over the alphabet {x, y, z} where the number of y’s is not divisible by 2 or 7 and no x appears after a z. This language is: |
| i ➥ recursively enumerable but not context-free |
| ii ➥ context-free but not regular |
| iii ➥ not known to be regular |
| iv ➥ regular |
Show Answer With Best Explanation
| Q45➡ |Regular Languages Given the following statements : S1 : If L is a regular language then the language {uv | u ∈ L, v ∈ LR} is also regular. S2 : L = {wwR} is regular language. Which of the following is true ? |
| i ➥ S1 is correct and S2 is correct. |
| ii ➥ S1 is correct and S2 is not correct. |
| iii ➥ S1 is not correct and S2 is correct. |
| iv ➥ S1 is not correct and S2 is not correct. |
Show Answer With Best Explanation
| Q46➡ |Regular Languages Consider the following two languages : L1 = {an bl ak | n + l + k>5 } L2 = {an bl ak | n>5, l >3, k≤ l } Which of the following is true ? |
| i ➥ L1 is not regular language and L2 is regular language |
| ii ➥ Both L1 and L2 are not regular languages. |
| iii ➥ Both L1 and L2 are regular languages. |
| iv ➥ L1 is regular language and L2 is not regular language. |
Show Answer With Best Explanation
| Q47➡ |Regular Languages Consider R to be any regular language and L1 .L2 be any two context-free languages Which one of the following is correct ? |
| i ➥ L 1 ⋂ L 2 is context free |
| ii ➥ L 1 is context free |
| iii ➥ L 1 − R is context free |
| iv ➥ (L 1 ⋃ L 2 ) − R is context free |
Show Answer With Best Explanation
| Q48➡ |Regular Languages The regular grammar for the language L = {w|na(w) and nb(w) are both even, w ∈ {a, b}*} is given by : (Assume, p, q, r and s are states) |
| i ➥ p → aq | br, q → bs | ap r → as | bp, s → ar | bq p is both initial and final states |
| ii ➥ p → aq | br | λ, q → bs | ap r → as | bp, s → ar | bq p is both initial and final states. |
| iii ➥ p → aq | br, q → bs | ap r → as | bp, s → ar | bq, p and s are initial and final states. |
| iv ➥ p → aq | br | λ, q → bs | ap r → as | bp, s → ar | bq, p and s are initial and final states. |
Show Answer With Best Explanation
| Q49➡ |Regular LanguagesConsider the following two languages: L 1 = {x | for some y with | y| = 2|x| ,xy∈ L and L is regular language} L 2 = { x | for some y such that |x| = |y|, xy∈ L and L is regular language} Which one of the following is correct? |
| i ➥ Only L 2 is regular language |
| ii ➥ Only L 1 is regular language |
| iii ➥ Both L 1 and L 2 are not regular languages |
| iv ➥ Both L 1 and L 2 are regular languages |
Show Answer With Best Explanation
| Q50➡ |Regular Languages Let R1 and R2 be regular sets defined over the alphabet, then |
| i ➥ R1 * is not regular |
| ii ➥ Σ * – R1 is regular |
| iii ➥ R1 ∪ R2 is not regular |
| iv ➥ R1 ∩ R2 is not regular |
Show Answer With Best Explanation
| Q51➡ |Regular Languages Consider R to be any regular language and L1.L2 be any two context-free languages Which one of the following is correct ? |
i ➥  |
ii ➥  |
iii ➥  |
iv ➥  |
Show Answer With Best Explanation
| Q52➡ |Regular Languages Regular sets are closed under |
| i ➥ Kleene’s closure |
| ii ➥ Union |
| iii ➥ Concatenation |
| iv ➥ All |
Show Answer With Best Explanation
| Q53➡ |Regular Languages Which of the following statements is correct? |
| i ➥ A={anbn |n= 0,1,2,3..} is regular language |
| ii ➥ L(A*B*) ∩ B gives the set A |
| iii ➥ Set B of all strings of equal number of a’s and b’s defines a regular language |
| iv ➥ none of these |
Show Answer With Best Explanation
| Q54➡ |Regular Languages The finite state machine given in figure below recognizes : 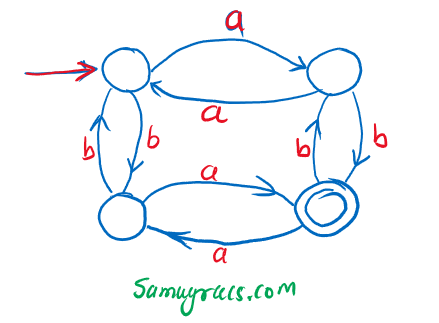 |
| i ➥ any string of odd number of a’s |
| ii ➥ any string of odd number of b’s |
| iii ➥ any string of even number of a’s and odd number of b’s |
| iv ➥ any string of odd number of a’s and odd number of b’s |
Show Answer With Best Explanation
| Q55➡ |Regular Languages Two finite state machines are said to be equivalent if they : |
| i ➥ Have the same number of states and edges |
| ii ➥ Recognize the same set of tokens |
| iii ➥ Have the same number of states |
| iv ➥ Have the same number of edges |
Show Answer With Best Explanation
| Q56➡ |Regular Languages Choose the correct statement: |
| i ➥ L(A * B) ∩ B gives the set A |
| ii ➥ The set B, consisting of all strings made up of only a’s and b’s having an equal number of a’s and b’s defines a regular language |
| iii ➥ A = {an bn | n = 1, 2, 3, …. } is a regular language |
| iv ➥ None of the above |
Show Answer With Best Explanation
| Q57➡ |Regular Languages All subsets of regular sets are regular. |
| i ➥ TRUE |
| ii ➥ FALSE |
Show Answer With Best Explanation
| Q58➡ |Regular Languages Regularity is preserved under the operation of string reversal. |
| i ➥ TRUE |
| ii ➥ FALSE |
Show Answer With Best Explanation
| Q59➡ |Regular Languages Choose the correct alternatives (More than one may be correct). Let R1 and R2 be regular sets defined over the alphabet Σ Then: |
| i ➥ R1 ∪ R2 is regular. |
| ii ➥ Σ* − R1 is regular. |
| iii ➥ R1 ∩ R2 is not regular. |
| iv ➥ R1* is not regular. |
Show Answer With Best Explanation
| Q60➡ |Regular Languages IMP* Consider the following statements. A. If L1 ∪ L2 is regular, then both L1 and L2 must be regular. B. The class of regular languages is closed under infinite union. Which of the above statements is/are TRUE? |
| i ➥ A only |
| ii ➥ B only |
| iii ➥ Both A and B |
| iv ➥ Neither A nor B |
Show Answer With Best Explanation
| Q61➡ |Regular Languages Which of the following statements is false? |
| i ➥ The intersection of two regular sets is regular |
| ii ➥ Every finite subset of a regular set is regular |
| iii ➥ Every subset of a regular set is regular |
| iv ➥ Every finite subset of a non-regular set is regular |
Show Answer With Best Explanation
| Q62➡ |Regular Languages Consider the following languages: L1 = {ww|w ∈ {a,b}*} L2 = {wwR|w ∈ {a,b}*, wR is the reverse of w} L3 = {02i|i is an integer} L4 = {0i2|i is an integer} Which of the languages are regular? |
| i ➥ Only L3 |
| ii ➥ Only L1 and L2 |
| iii ➥ Only L2, L3 and L4 |
| iv ➥ Only L3 and L4 |
Show Answer With Best Explanation
| Q63➡ |Regular Languages If s is a string over (0 + 1)* then let n0(s) denote the number of 0’s in s and n1(s) the number of 1’s in s. Which one of the following languages is not regular? |
| i ➥ L = {s ∈ (0+1)* | n0(s) mod 7 = n1(s) mod 5 = 0} |
| ii ➥ L = {s ∈ (0+1)* |n0(s) – n1(s)| ≤ 4} |
| iii ➥ L = {s ∈ (0+1)* | for every prefix s’ of s,|n0(s’) – n1(s’)| ≤ 2} |
| iv ➥ L = {s ∈ (0+1)* | n0(s) is a 3-digit prime} |
Show Answer With Best Explanation
| Q64➡ |Regular Languages Which of the following languages is regular? |
| i ➥ {xwwR|x, w ∈ {0,1}+} |
| ii ➥ {wxwR|x, w ∈ {0,1}+} |
| iii ➥ {wwRx|x, w ∈ {0,1}+} |
| iv ➥ {wwR|w ∈ {0,1}+} |
Show Answer With Best Explanation
| Q65➡ |Regular Languages Which of the following is TRUE? |
| i ➥ Infinite union of finite sets is regular. |
| ii ➥ The union of two non-regular sets is not regular. |
| iii ➥ Every finite subset of a non-regular set is regular. |
| iv ➥ Every subset of a regular set is regular |
Show Answer With Best Explanation
| Q66➡ |Regular Languages Let P be a regular language and Q be a context-free language such that Q ⊆ P. (For example, let P be the language represented by the regular expression p*q* and Q be [pnqn | n ∈ N]). Then which of the following is ALWAYS regular? |
| i ➥ Σ* – Q |
| ii ➥ Σ* – P |
| iii ➥ P – Q |
| iv ➥ P ∩ Q |
Show Answer With Best Explanation
| Q67➡ |Regular Languages Which of the following language is/are regular ? L1: {wxwR ⎪ w, x ∈ {a, b}* and ⎪w⎪, ⎪x⎪ >0} wR is the reverse of string w L2: {anbm ⎪m ≠ n and m, n≥0} L3: {apbqcr ⎪ p, q, r ≥ 0} |
| i ➥ L3 only |
| ii ➥ L2 only |
| iii ➥ L1 and L3 only |
| iv ➥ L2 and L3 only |
Show Answer With Best Explanation
| Q68➡ |Regular Languages Language L1 is defined by the grammar: S1 → aS1b|ε Language L2 is defined by the grammar: S2 → abS2|ε Consider the following statements: P: L1 is regular Q: L2 is regular Which one of the following is TRUE? |
| i ➥ Both P and Q are false |
| ii ➥ P is false and Q is true |
| iii ➥ P is true and Q is false |
| iv ➥ Both P and Q are true |
Show Answer With Best Explanation
| Q69➡ |Regular Languages Which of the following languages is generated by the given grammar? S→ aS|bS|ε |
| i ➥ {a,b}* |
| ii ➥ {anbm |n,m ≥ 0} |
| iii ➥ {w ∈ {a,b}* | w has equal number of a’s and b’s} |
| iv ➥ {an |n ≥ 0}∪{bn |n ≥ 0}∪{an b(sup>n|n ≥ 0} |
Show Answer With Best Explanation
| Q70➡ |Regular Languages For Σ = {a,b}, let us consider the regular language L = {x|x = a2+3k or x = b10+12k, k ≥ 0}. Which one of the following can be a pumping length (the constant guaranteed by the pumping lemma) for L? |
| i ➥ 4 |
| ii ➥ 8 |
| iii ➥ 6 |
| iv ➥ 24 |
Show Answer With Best Explanation
| Q71➡ |Regular Languages If L is a regular language over Σ = {a,b}, which one of the following languages is NOT regular? |
| i ➥ L ∙ LR = {xy │ x ∈ L, yR ∈ L} |
| ii ➥ Prefix (L) = {x ∈ Σ*│∃y ∈ Σ* such that xy ∈ L} |
| iii ➥ {wwR │w ∈ L} |
| iv ➥ Suffix (L) = {y ∈ Σ* such that xy ∈ L} |
Show Answer With Best Explanation
| You should also practice on below topics Regular Language Mode Deterministic Finite Automaton (DFA), Non-Deterministic Finite Automaton (NDFA), Equivalence of DFA and NDFA, Regular Languages, Regular Grammars, Regular Expressions, |
