Data Structure Test Set 10
| Q46➡ | In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges. The number of connected components in G is |
| i ➥ k |
| ii ➥ k + 1 |
| iii ➥ n – k – 1 |
| iv ➥ n – k |
| Q47➡ | The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is 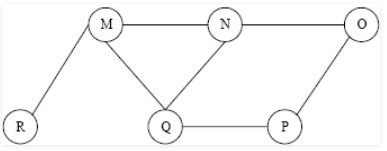 |
| i ➥ MNOPQR |
| ii ➥ NQMPOR |
| iii ➥ QMNPRO |
| iv ➥ QMNPOR |
| Q48➡ | Let G be a graph with n vertices and m edges.What is the tightest upper bound on the running time of Depth First Search on G, when G is represented as an adjacency matrix? |
| i ➥ Θ(n) |
| ii ➥ Θ(n+m) |
| iii ➥ Θ(n2) |
| iv ➥ Θ(m2) |
| Q49➡ | The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity |
| i ➥ Θ(n) |
| ii ➥ Θ(m) |
| iii ➥ Θ(m+n) |
| iv ➥ Θ(mn) |
| Q50➡ | Consider the following graph: Among the following sequences: (I) a b e g h f (II) a b f e h g (III) a b f h g e (IV) a f g h b e Which are depth first traversals of the above graph? |
| i ➥ I, II and IV only |
| ii ➥ I and IV only |
| iii ➥ II, III and IV only |
| iv ➥ I, III and IV only |
Weekly Test GATE/NTA NET CSA

47:iv
46, ii
47, ii
48, iii
49, i
50, i